논문명 : Plenoxels: Radiance Fields without Neural Networks
Scene별 Optimization(학습) 속도를 대폭 향상시킨 연구중 하나입니다.
저자 메인 사이트에 공개된 영상을 보면 6초만에 어느 정도의 윤곽을 보이고, Point-NeRF와 같이 2분이면 선명한 결과를 보입니다.
최초 NeRF에서는 1.6일간 PSNR 31.15을 달성했던 것을 Ploenoxel에서는 11분만에 PSNR 31.83을 달성합니다.
Main Approach는 크게 2가지 입니다.
- 기존 NeRF논문들과 다르게 Neural Network를 쓰지 않았고 Voxel Grid에 Trilinear Interpolation기법으로 Direct Optimization하였습니다.
- Regularization을 통해 퀄리티를 향상시켰습니다.
본 글에서 Plenoxels 논문에 대해 상세하게 다뤄보겠습니다.
Algorithm
Plenoxels의 전체구조는 다음과 같습니다.
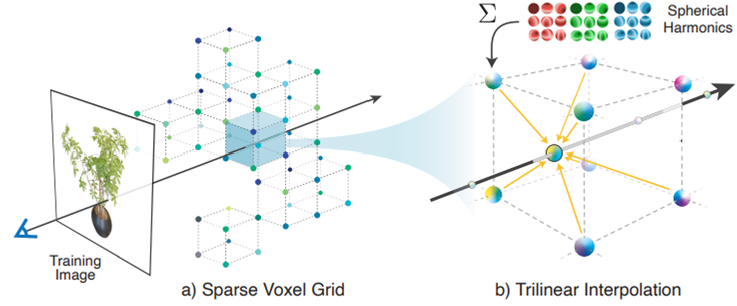
256^3해상도의 Voxel Grid를 구성합니다. 각 voxel은 3차원 좌표 index(key값)으로 Spherical Harmonics coefficient와 Volume Density값(value값)으로 구성된 3D index array로 설계합니다.
설명을 위해 PlenOctree를 참조하자면, Ray위에 샘플링한 각 voxel에 대해 Volume Desity σ 와 Coefficient k , View direction (θ, Φ)으로 pixel의 color를 계산 할 수 있었습니다. 자세한 내용은 PlenOctree 논문 이전 포스트 글을 확인바랍니다.

Plenoxels에서는 Network를 사용하지 않고, σ와 k를 직접적으로 Optimize합니다.
Network가 사라지면서 Weight가 없는데 Optimization이 가능한가?라고 의문이 될텐데, 일단 Index Array의 Value인 SH coefficient와 volume density가 학습 paprameter가 됩니다. 추가적인 기법에 대해서는 세부적으로 어떻게 설계 하였는지 소개 드리겠습니다.
Trilinear interpolation
2D plane에서 3D영역으로 Ray를 그리면, ray는 voxel grid의 voxel들을 정확히 지나가지 않습니다. Ray위에 샘플링한 voxel들을 3D index array의 index (key) 좌표값을 갖고 있는 주변 8개의 voxel 위치(x,y,z)에 대한 값(σ, k)으로 부터 interpolation합니다.
논문에서는 Interpolation 기법을 적용한 근거로 nearest neighbor기법과 Interpolation기법을 비교하였습니다. 1) Optimization을 위해 Continous function을 사용하고 2) Learning rate variation관점에서 좀더 안정적이고, 3) 효과적으로 resolution 증가 가능하기 때문에, Interporlation 방법을 사용했다고 합니다.
Optimization
Predicted된 이미지의 pixel color와 GT 이미지간의 MSE(Mean Squared Error)값과 total variation(TV) regularization값으로 Loss Function을 설계하였습니다. λTV는 상수값입니다.

Reconstruction Loss는 최초 NeRF와 동일하게 Rendering한 결과 pixel간의 차이 값입니다.

TV regularization Loss는 다음과 같습니다.
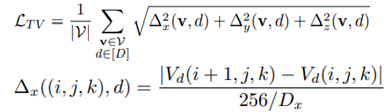
아래식에서 Vd의 인자인 i,j,k는 각각 x,y,z를 나타내고, Vd의 출력값은 위에서 언급한 3D index array에 저장하고 있는 density(σ), SH coefficient(k) 값입니다. Δx는 x에 관한 식이라서 왼쪽 Vd의 인자가 (i+1, j, k) 이고, y에 관한식이라면 Vd의 인자는 (i, j+1, k) 가 될 것입니다. 옆 voxel값과의 차이를 나타내는 식이라 보면 됩니다. D는 각 dimension의 grid 해상도를 나타내며, 이미지 크기로 normalization이 됨을 의미합니다. d는 Vd가 저장하고 있는 차원크기입니다. Density의 경우 1이 될 것이고, Sh coefficient는 9개가 됩니다(SH degree가 2이기 때문). Δx 는 특정 좌표에서 x dimension의 인접한 voxel간의 값(σ, k)의 차이를 나타냅니다.
결과적으로 LTV는 샘플링 된 voxel에 대해, dimension각각의 인접한 voxel간의 차이값으로 표현됩니다.
빠른 itertation을 위해서 각 optimization step시에, Recon term을 evaluation하기 위해 ray R를 stochastic sampling하고, TV term을 evaluation하기 위해 voxel V도 stochastic하게 sampling하였다고 합니다. JAXNeRF, Mip-NeRF와 같은 learning rate로 스케쥴링을 사용하였습니다. 초기 learning rate는 opacity와 harmonic coefficient를 따로 분리하고, main 실험에서는 고정된 learning rate를 사용하였습니다.
이게 학습된 Weight(Volume Desity σ 와 Coefficient k)는 Scene type(bounded, forward-facing, 360도)마다 고정됩니다.
Direct Optimization Issue & Solution
Voxel coefficient를 직접적으로 optimizing하는 것은 아래와 같은 문제가 있었습니다.
- Optimize할 value(256^3 * (1+9))가 너무 많았습니다. -> high-dimensional problem
- (rendering 방법으로 인해) Optimization objective가 nonconvex였습니다. -> objective가 convex하면 함수의 global minima가 1개 있는 것이고, nonconvex하면 2개 이상이 존재합니다. (https://100s.tistory.com/31)
- Optimization objective는 poorly conditioned였습니다. -> 함수에 차원이 많을수록 영향력 있는 Gradient를 가진 차원을 찾기가 어려워 학습이 오래걸립니다 . (https://velog.io/@guide333/%ED%92%80%EC%9E%8E%EC%8A%A4%EC%BF%A8-CS231n-7%EA%B0%95-Training-Neural-Networks-Part-2-1)
Pooly conditioning은 2차 미분함수를 사용하는 second-order optimization algorithm으로 해결됩니다. (일반적인 gradient descendent는 1차 미분함수입니다, https://iopscience.iop.org/article/10.1088/1757-899X/495/1/012003/pdf)
하지만 이 문제는 Hessian(2차 미분 행렬)이 너무 커서 각 step에서 쉽게 계산되지 않고, 역함수를 만들기가 쉽지 않기 때문에, high-dimensional problem을 해결하는 것이 어려웠습니다.
이러한 ill-conditioning problm을 Plenoxels에서는 RMSProp Optimization를 사용해서 second-order 함수의 full computational complexity없이 해결 하였습니다. RMSProp Optimization는 복잡한 다차원 곡면 함수를 잘 탐색하도록, 기울기를 단순 누적하지 않고 지수 가중 이동 평균 Exponentially weighted moving average 를 사용하여 최신 기울기들이 더 크게 반영되도록한 Optimization 방법입니다. (RMSProp : https://light-tree.tistory.com/141)
Regularization

다음으로 Regularization 효과와 Scene type별 Regularization에 대해 소개하겠습니다.
TV(total variation) regularization은 Rendering 결과를 smooth하게 만들어줍니다.
위 이미지는 TV regularization을 넣었을 경우(Full), SH의 TV를 제외하였을 경우(No SH TV), density TV를 제외하였 경우, TV를 모두 제외 하였을 경우를 비교하는 결과입니다. (PSNR평가지표를 통해서는 이러한 차이를 못잡아 낸다고 합니다.)
모든 scene에서 사용되는 TV regularization에 추가적으로 특정 scene type에서 regularizer를 사용했습니다.
Real, forward-facing, 360 scene에서, SNeRG논문의 Cauchy loss에 기반한 saprsity prior를 사용했습니다.

Σlog( )부분은 training ray i 위에 샘플링된 k번째 voxel의 opacity를 나타냅니다.
Forward-facing scene에서 optimization을 위한 각 minibatch에 대해, 각 active ray 위의 각 sample에서 loss term을 평가하였습니다.
PlenOctrees에서 사용한 sparsity loss와 유사하게, voxel이 empty가 되도록 해줍니다.
Upsampling할 때, Memory를 절약하고 quality loss를 줄여주도록 도와줍니다.
Real 360도 scene에서는, 각 minibatch내 각 ray의 accumlate된 foreground transmittance위에서 beta distribution regularizer를 사용했습니다.

r은 Training ray이고, Tfg(r)은 ray r의 accumulated foreground transfittance (0~1사이값)입니다.
(Neural Volumes를 따르는) beta loss term은 foreground가 fully opaque 또는 empty 둘 다 될 수 있도록 함으로써, clear하게 forground와 background분해를 할 수 있도록 만들어 줬습니다.
두번째는 background만 랜더링, 세번째는 forground만 랜더링했을 때 이미지입니다.

여기까지가 메인 아이디어인 Trilinear interpolation을 사용한 Optimization기법과 Regularization기법에 대한 컨셉을 설명하였고, 아래에서 High Resolution을 만들기 위한 상세 기법, Unbounded scene생성 방법에 대해 소개합니다.
Coarse to Fine
- 256^3해상도의 dense grid를 만듭니다.
- PlenOctree의 Voxel Pruning(Filtering)기법과 유사한 방법으로 Voxel을 제거 합니다. (각 Ray내 voxel들의 불투명도(=Ti(1-exp(−σiδi))) 최대값을 유지하면서, Threshould보다 낮은 weight를 가진 voxel grid을 제거합니다.)
- 각 dimension을 반으로 나눠서 남아있는 voxel을 refine합니다.
- 512^3해상도로 upsampling됩니다. (임의의 해상도로도 변경 가능합니다.)
- 빈 공간들을 Trilinear interpolation합니다.
이 학습 과정엔 한가지 문제가 있는데, Pruning된 point들은 surface내부의 가장 가까운 voxel들과 interpolation할 때, surface 주변의 color와 density에 영향을 미칠 수 있습니다. 이를 위해서, pruning 대상 voxel과 그 이웃이 unoccupied되어 있을 때만, voxel를 pruning 합니다.
Unbounded Scenes
최초 NeRF의 synthetic scenes을 넘어 wide range 환경에서도 optimize할 수 있었습니다. Minor한 변형을 통해, real, unbounded scene, forward-facing, 360도 scene으로 확장했습니다. Forward Facing Scene에서는 normalized device coordinates에서 sparse voxel grid structure를 사용하였습니다.
360도 Scene을 위해, MSI(Multi-Sphere Image) background model을 사용하여 sparse voxel grid foreground representation을 augment하였습니다. MSI model은 360도 이미지가 겹겹히 쌓인 모델로써, 원점이 같고 반지름이 다른 구에 맺히는 360도 이미지들 이라고 생각하면 됩니다.(https://visual.cs.brown.edu/projects/matryodshka-webpage/)
sphere들 내부 또는 sphere들 간의 voxel color와 opacity값으로 trilinear interpolation 합니다. Simple equirectangular projection을 사용해서 voxel들이 sphere으로 warp(변형)되는 것을 제외하면, 이것은 Forground Model과 같습니다. (Simple equirectangular projection는 지구(Sphere)를 지도(image)로 표현할 때 사용하는 projection입니다.)

64개 sphere는 linearly하게 단위 벡터인 1부터 1/무한대까지 radius로 위치하게 됩니다. (sphere안의 inner scene에 대해 scale을 조절하였습니다.) Memory를 위해, color를 rgb channel로 저장하고, Main model과 동일하게 opacity thresholding을 사용함으로써 모든 레이어를 sparsely하게 저장하였습니다. 이러한 방법은 NeRF++의 background model과 유사합니다.
위에 글은 논문 내용을 최대한 풀어 옮긴 내용이고, 아래는 그 의미를 개인적으로 재해석한 의견입니다.
64개의 겹겹히 쌓여져 있는 구를 가상으로 만들고, 그 구의 표면에 있는 voxel들의 color와 density값을 interpolation을 통해 계산합니다. 이를 통해, foreground 이미지는 구 내측의 voxel들의 값으로 랜더링하고, background이미지는 구 외측의 voxel들의 값으로 랜더링 하지 않을까 싶습니다.
Implementation
Plenoxel model의 gradient는 매우 sparse하고 빠르기 때문에 large part안에서 possible한(납득 가능한) 속도를 보였습니다. 1-2분의 Optimization을 하면 10%이하의 voxel이 nonzero gradient를 갖게 됩니다.
Results

Synthetic Scenes(상단)

(NeRF에서 공개한 Blender로 생성한) 8개Scene에 대해 800x800 해상도 100개의 이미지로 학습했습니다.
Scene마다 평균 11분 소요 되었습니다.
Forward-facing scene (중간)

NDC(normalized device coordinates)를 사용해서 unbounded인 forward-facing scene을 확장했습니다.
Optimization을 통해 (강한 weight로) TV regularization을 사용한 것을 제외하고 bounded인 synthetic scene과 동일한 방법을 사용했습니다. 적은 수의 Training view 때문에 이러한 변화는 필수적이었습니다.
각 SCene은 1008x756해상도로, 20~60개의 forward-facing image로 구성되었습니다. 7/8은 학습데이터, 나머지는 트레이닝 데이터 셋입니다. 각 input view에 한 개 grid를 predict하는 3D CNN을 사용한 방법인 LLFF(Local Light Field Fusion)방법과 비교하였습니다.
Real 360도 Scenes(하단)

MSI(multi-sphere image) 로 sparse voxel grid를 surrounding 함으로써 real한 unbunded된 360도 scene을 확장했습니다. (각 background sphere는 trilinear interpolation을 가진 simple voxel grid입니다.)
Tank&Temple dataset으로 4개 Scene을 사용했습니다.
Unbounded scene을 표현하기 위해 background model로 증강시킨 NeRF++와 비교하였습니다.
저자가 올린 영상 결과물입니다.
Ablation Studies
Training image 수를 100에서 25로 줄였을 때 실험 결과를 비교하였습니다.
(평가지표 의미 : PSNR/SSIM/LPIPS 글 참조)

Real scene은 적은 training image를 가지고 Higher TV regularization는 optimization이 sparsely-supervised regions로 확장을 도울 수 있었기 때문에, real forward-facing scene에서 더 좋은 성능을 보였습니다.
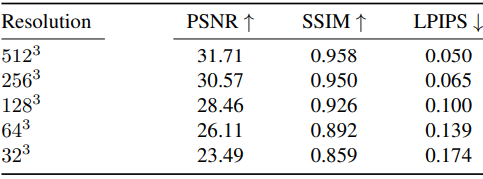
Plenoxel grid resolution에 따른 결과 입니다.
Rendering formular를 비교하였습니다.

NeRF를 사용하고 Plenoxel의 main method를 사용한 Max와 Relative transmittance 대신에 absolute를 사용한 Neural Volumes를 비교하였습니다.
Closing..
Neural Network를 사용하지 않고, 직접적으로 coefficient와 volume density를 학습하는 모델을 만들었습니다. Optimization 속도가 빠르니, 입력으로 필요한 이미지 갯수가 많아야 한다는 것이 아쉽게 느껴지네요. 필요 입력 이미지 수를 1~3장으로 줄이면서, 속도까지 개선된 논문이 나오기를 기대해봅니다.
'NeRF' 카테고리의 다른 글
| [논문 리뷰] Instant NGP(SIGGRAPH 2022) : 인코딩 방법 개선으로 속도 향상 (2) | 2022.11.10 |
|---|---|
| [논문 리뷰] MVSNeRF (ICCV2021) : 적은 입력 + 학습 속도 개선 논문 (0) | 2022.10.27 |
| [논문 리뷰] Point-NeRF (CVPR 2022) : 학습 속도 개선 논문 (1) | 2022.10.13 |
| [논문 리뷰] PlenOctrees for NeRF (ICCV 2021) : 랜더링 속도 개선 논문 (4) | 2022.10.12 |
| [논문 리뷰] PixelNeRF (CVPR 2021) : 입력 이미지 갯수를 개선한 NeRF 연구 (0) | 2022.10.11 |




댓글