PhysGaussian: Physics-Integrated 3D Gaussians for Generative Dynamics, Tianyi Xie, CVPR 2024
물리 시뮬레이션 개념을 3D Gaussian Splatting에 적용한 연구입니다. 3D Gussian에 부피, 질량, 속도 속성을 넣고 시간에 따른 변화를 모델링하는 연구입니다. 결과물이 재밌습니다.
작동 원리를 파악해보겠습니다.
Overview
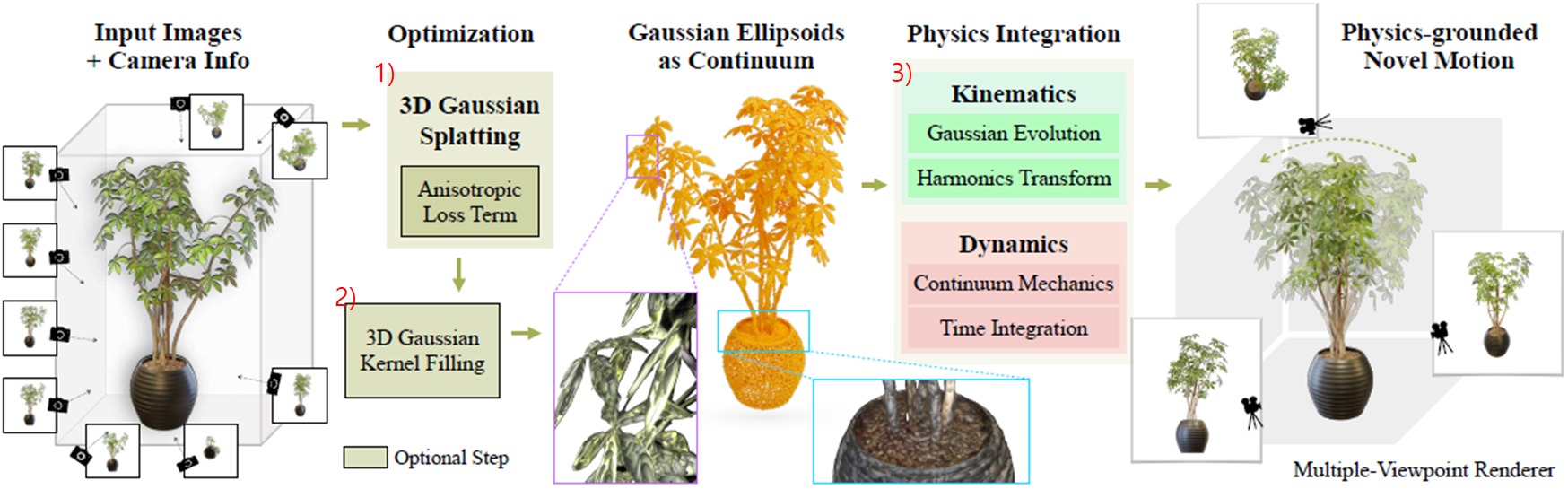
1) 3D Gaussian Splatting 모델을 만들 때, Anisotropic Loss로 3D Gaussian을 둥글게 만듭니다.
2) Object 내부 공간을 3D Gaussian으로 채웁니다.
3) Physics Simulation을 사용하여 모델링합니다.
- 3D Gaussian에 부피, 질량을 부여하여 Continum Mechanics(연속체 역학)을 따르도록 만듭니다.
- 시간 변화에 따른 물리적인 (Kinematics=운동학) 변화를 Gaussian 3D Gaussian으로 모델링합니다.
용어 정리
Continuum Mechanics(연속체 역학)에 대한 개념을 선행지식으로 언급하고 있습니다.
Conservation of mass(질량 보존 법칙)
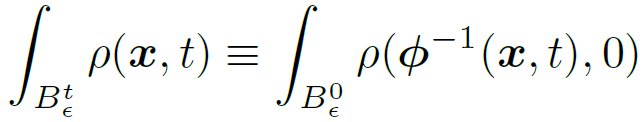
시간이 바뀌어도 특정 물질 영역내 질량은 항상 일정하게 유지된다라는 것을 설명하는 수식입니다.
$ B_{\epsilon}^t$는 시간t에서 변형된 world space 내의 극소 영역(=infinitesimal=무한소)
$ B_{\epsilon}^0$는 초기 상태이며, material space 내의 극소 영역. (material space를 초기상태로 생각하면 읽기 편합니다.)
$ \rho(x, t)$는 시간 t에서 위치 x의 밀도 필드이며 물질의 분포를 나타냄
$ \phi(x, t) $는 시간 t에서 material space에서 world space로 변형하는 deformation map(변형 맵)
conservation of momentum(운동량 보존 법칙)
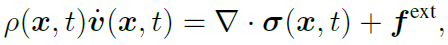
연속체 역학에서 물질의 운동량은 시간에 따라 변하지 않음을 설명하는 수식입니다.
$ \rho(x, t) $는 시간t에서 위치 x의 밀도 필드 (=density field)
$ v(x, t) $는 시간 t에서 위치 x의 속도 필드 (=velocity field)
$ \dot{v}(x, t) $는 시간 t에서 위치 x의 가속도 필드
$ \nabla \cdot \sigma(x, t)$는 시간 t에서 위치 x의 응력 텐서(=Cauchy stress tensor=물질 내부힘 6방향)의 변화량
$ \mathbf{f}^{\text{ext}}$는 외부에서 작용하는 단위 부피당 힘
여기서 응력은 hyperelastic energy density(초탄성 에너지 밀도)로 계산되어지며,deformation(변형)은 원래 형태로 되돌아 오는 성질을 가지는 elastic part(탄성)과 복원하지 못하는 plastic part(소성)으로 나뉘어 집니다.
Material Point Method (MPM)
연속체 물질의 변형을 시뮬레이션하는 기법으로 Lagrangian Particles(라그랑지안 입자)와 Eulerian Grid(오일러리안 그리드)의 조합으로 구성되어 있습니다. Lagrangian Particles는 입자의 위치,속도, 진량, 변형 상태의 물리적 속성을 모델링하고 입자별로 추적하고 정보를 업데이트하는 방식입니다. Eulerian Grid는 공간을 그리드로 나누고 그리드를 통해 입자를 이동시키는 방식입니다.
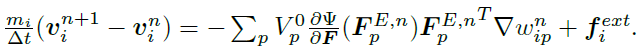
위 수식은 MPM에서 운동량 보전을 설명하는 수식입니다. v는 속도 p는 입자, F는 deformation gradient, f는 외부힘을 나타내며 자세한 수식은 생략하겠습니다. 입자와 그리드간에 운동량이 상호작용하며 이 과정에서 질량과 운동량이 보존되도록 하여 물리적 일관성을 유지하고 시뮬레이션의 정확도를 높여 현실적인 결과를 얻을 수 있게 한다는 포인트만 알고 넘어가면 됩니다. 그 외 별도의 글(이전글)로 MPM 방식에 대해 정리해두었습니다.
Physics-Integrated 3D Gaussians
3D Gaussian Splatting(이전글)에 Physics특성을 결합하는 방법에 대해 소개합니다. 기존 3DGS의 3D Gaussian 수식(이전글)을 동일하게 들고 갑니다.

시간에 따른 deformation을 위해 시간 t가 추가 됩니다.

$\phi(x, t)$는 질량 보존의 법칙 설명에서 한번 언급된 기호며, 시간 변화에 따른 deformation map입니다. point가 변형되는 정도를 나타내는 array로 생각하면 될 것 같습니다. 이에 대한 역행렬은 변형 전 초기상태를 나타냅니다. 이를 계산가능한 수식으로 만들기 위해, local affine transformation가 가능하도록 $\phi$를 1차 근사식으로 바꿉니다.
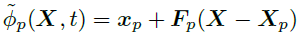
$ X $ 는 임의점의 위치
$ x_p $ 는 입자p의 현재 위치
$ X_p $ 는 입자p의 변형 전의 초기 위치
$ X - X_p $는 입자p 기준으로 X에 대한 상대 위치 벡터
$ F_p $ 는 점 $X$가 어떻게 이동했는지에 대한 deformation gradient 행렬
입자 $x_p$ 를 기준으로 임의점 X들이 시간t가 변했을 때, 얼마나 이동했는지를 나타낸 수식이라 생각하면 됩니다.
해당 수식을 기반으로 3DGS에 적용하면 3D Gaussian의 position X와 covariance matrix(=scale*rotation) A행렬이 아래와 같이 변화됩니다.
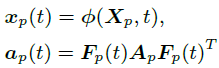

$F_p$는 각차원 scale,rotation에 영향을 주게되므로, A의 앞뒤로 곱해집니다. 이러한 형태는 Covariance matrix특성 때문입니다(이전글 참고). 이를 적용한 PhysGaussian 수식은 아래와 같습니다.

배경셀 부피를 포함된 입자수로 나누어서 각 particle 부피 $ V_0^p$를 초기화하고 사용자가 지정한 밀도 $\phi_p$를 사용하여 질량 $m_p = \phi_pV_0^p$을 계산하여 사용합니다.
정리하자면, 위와 같이 설계를 통해, 가우시안은 질량을 가지게되고 MPM시뮬레이션을 바탕으로 물리법칙(질량보존,운동량보존)을 따르게 만들었다는 의미로 볼 수 있습니다.
이 부분에서 저자는 물리학과 가우시안 통합이 매끄럽다라는 점을 강조하고 있습니다.
1) 가우시안 자체는 연속체의 이산화된 형태로 간주되기 때문에 직접적으로 시뮬레이션 될 수 있습니다.
2) 변형된 가우시안은 스플래팅 과정에 의해 직접적으로 랜더링 될 수 있습니다.
이는 실제 데이터로부터 재구성을 직접적으로 시뮬레이션 할 수 있어 WS2(What you see is What you simulate)를 달성했다고 합니다.
Spherical Harmonics의 Orientations
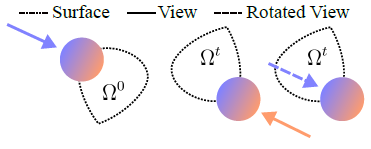
3DGS의 color는 view direction마다 다른 값을 표현하는 Spherical Harmonics(이전글)로 모델링되어 있습니다. 때문에 t에 따라 입자가 움직이면서 회전하게 되면 색상이 전혀 달라지게됩니다. 3DGS 프레임워크에 SH부분이 하드코딩되어 있어서, 저자는 view direction(시야 방향)에 역회전을 적용하였다고 합니다.
이렇게만 설명되어 있어서 제 생각을 적어보자면, 위에 첫번째 이미지는 초기 상태인데, 회전이 되면서 2번째 이미지가 됩니다. 그럼 주황색에서 바라 본 색상은 전혀 다른 엉뚱한 색상이 되는데, 주황색 view direction을 쓰지 않고, 입자가 회전된만큼 SH함수의 입력값을 회전시켜서, 가상의 3번째 점선 view direction값으로 사용한다는 의미로 받아 들였습니다.
그럼 입자의 회전 정보를 어떻게 알 수 있는가가 문제인데, 이전 연구인 Point-NeRF에서는 surface orientation을 사용했었지만 본 논문에서는 deformation gradient인 $F_p$를 사용했다고 합니다. polar decomposition을 통해 $F_p$에서 $F_p = R_pS_p$ rotation과 scale값을 분리해서 R값을 사용 할 수 있습니다.
Incremental Evolution of Gaussians
앞서 언급한 $F$는 Guassian과 physics 시스템이 어떻게 결합하는지에 대해 설명하기 위함이고, 실제적으로는 F는 사용하지 않습니다. F가 포함된 covariance matrix부분이 아래와 같이 변형됩니다.
deformation gradient $F$의 의존성을 피하고 Gaussian Kinematic(운동학)에 잘 맞는 다른 Lagrangian framework(=물질을 시뮬레이션하는 MPM의 기법)을 제안하고 있습니다. computational fluid dynamics(전산 유체 역학)에 따라 covarance matrix a 는 discretizing되어 속도 v와 시간 t의 변화량으로 구성합니다.
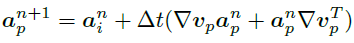
deformation Rotation matrix의 경우 초기 R은 I로 초기화하고, 아래 수식으로 업데이트 됩니다.
$$ R_p^{n+1} = \left( I + \Delta t \mathbf{v}_p \right) R_p^n$$
Internal Filling
3D Gaussian은 표면 가까이에만 존재합니다. deformation이 클 경우 내부가 노출 될 수 있으므로 내부를 채워주는게 필요합니다. particle을 내부에 채우기 위해 3D opacity filed를 사용합니다.

3D Gaussian 확률밀도 함수에서 opacity가 들어간 형태입니다. 아래 두가지 조건이 맞으면 내부로 간주하고 3D Gaussian을 생성합니다.

일정 간격의 grid를 그려 각 grid의 셀을 선택하고, 해당 지점에서 6방향으로 ray를 그려 lower opacity와 high opacity를 지나는지 intersection 갯수로 산정합니다. 새로 생성되는 3D Gaussian은 인접한 값을 사용하고, 부피값으로 반지름을 계산하여 3개축을 동일한 반지름으로 사용합니다. $ r_p = \left( \frac{3V_p^0}{4\pi} \right)^{\frac{1}{3}} $ 부피값은 "Physic Integrated 3D Gaussian"섹션에서 언급됬었습니다.
Anisotropy Regularizer
아주 얇은 3D Gaussian은 물체 표면에서 바깥쪽으로 튀어나와 artifact를 만들 수 있습니다. 때문에 둥글게 만들어주기 위해 추가한 regularization term입니다. 주축의 길이와 부축의 길이 비율이 r을 초과하지 않도록 제한합니다.

Experiments
Dataset : fox, plane, runis는 각각 순서대로 InstantNGP, NerfStudio, DroneDeployNeRF에서 갖고왔고, toast와 jam은 iphone에서 150장으로 촬영했다고 합니다. MPM은 link 를 사용했다고 합니다. 수작업으로 simulation 영역을 2x2x2길이의 큐브로 선택하고 normalize했습니다. length 2라고만 표현되어 있는데, scale을 알 수 없으므로 임의의 크기라고 생각되어집니다. 해당 구간에 대해서만 particle filling을 수행했습니다. 그리고 선택적으로 구체적인 입자를 선택하고 속도를 변형하였습니다. i9-10920X와 3090 GPU하나만 사용했습니다.
fox 결과 : 물체의 원래 형태가 변하지 않는 Elasticity(탄성) 성질을 적용하였습니다.
plane 결과 : 물체의 원래 형태가 영구적으로 변하는 Metal(금속) 성질을 적용하였습니다.
ruins 결과 : Druker-Prager plastic 모델을 따라 granular-level frictional effect(입자간의 마찰 효과)를 만들었습니다. 논문에서 Sand효과로 소개하고 있습니다.
toast 결과 : MPM시뮬레이션에 의해 자연스럽게 지원되며, 큰 deformation이 발생하면 입자가 여러 그룹으로 분리(Fracture) 됩니다.
jam 결과 : Herschel Bulkley plasticity 모델을 사용해 non-Newtonian fluid(비뉴턴성 점소성 유체)를 모델링했습니다. 논문에서 Paste효과로 소개하고 있습니다.
fox는 30FPS, toast는 25FPS, jam은 36FPS의 속도를 보였습니다.
여기까지가 정성적인 결과라면 다음은 정량적인 결과를 나타내고 있습니다.

post deformation에 대한 GT가 없기 때문에, BlenderNeRF를 사용해서 scene을 합성하고 latice deformation 을 사용해서 bending하고 twisting했습니다. 변형되지 않은 상태에서 100개 뷰를 랜더링하고, 각 변형 상태의 다중 뷰 랜더링 100개를 생성합니다.
3가지 모델과 비교하고 있습니다.
- NeRF-Editing 은 NeuS를 사용하고 추출된 surface mesh를 사용해서 NeRF를 변형합니다. surface reconstruction에 초점이 맞춰진 연구이기 때문에, rendering 퀄리티가 낮았습니다. deformation은 추출된 surface mesh와 cage mesh의 정밀도에 의존하게 됩니다. 그래서 경계가 공백으로 될 수 있습니다.
- Deforming-NeRF에서는 cage mesh를 사용해서 변형합니다. PAC NeRF는 개별 초기 입자를 조작했습니다. 고해상도 deformation cage를 통해 향상된 결과를 보였었지만, local detail를 filtering하면서 성능이 낮아졌습니다.
- PAC-NeRF는 단순한 object, texture를 가지도록 디자인 되었습니다. 입자 표현을 통해 flexibility를 제공하지만 높은 랜더링 퀄리티는 달성하지 못했습니다.
본 연구에서는 zero-order information(=deformation map)과 first-order information(=deformation gradient) 모두를 활용하였기 떄문에 변형 후에도 높은 성능을 보이게 됩니다.
Ablation Study는 아래 3가지 케이스에 대해 실험을 하였지만 큰 차이는 없습니다.
1) Fixed Covariance는 3D Gaussian의 covariance를 그대로 사용한 case입니다.
2) Gaussian의 transformation을 적용한 case입니다. (정확한 의미는 모르겠습니다.)
3) SH의 방향을 rotation하지 않은 case입니다.

시각적으로는 약간의 차이를 보입니다. 위 기법이 모두 적용되지 않았을 경우, 가우시안이 표면을 제대로 덮지 않게되며 artifact가 발생하게 되는 것을 보여줍니다.
Limitation
그림자를 고려하지 않고 있으며, material 매개변수가 수동으로 설정되고 있습니다. 자동 매개변수 할당은 3D 분할과 MPM 시뮬레이터를 결합하여 비디오에서 만들 수도 있습니다. geometry 인식 3DGS 방법을 통합하면 생성 동역학이 향상될 수 있습니다. 다양한 material를 처리하고 직관적인 사용자 제어를 통합 또는 LLM을 활용하는 하는 것을 향후 연구 주제로 둘 수 있습니다.
Closing..
NeRF와 3DGS는 전혀 다른 계열의 연구와 통합되는 형태가 많아보입니다. 그중에서 하나 재밌는 사례를 찾은 것 같습니다. 후속 논문들은 더 재밌는 사례를 보여주지 않을까합니다.
'3D-GS' 카테고리의 다른 글
| [논문 리뷰] Grendel-GS (arXiv2024) : Multi GPU로 3DGS (0) | 2024.08.10 |
|---|---|
| [논문 리뷰] Mip-Splatting (CVPR2024) : Anti-aliasing 기법 (0) | 2024.07.28 |
| [논문 리뷰] VastGaussian (CVPR 2024) : Large Scene (0) | 2024.06.17 |
| [논문 리뷰] GaussianEditor (CVPR2024) : 3D inpainting 연구 (2) | 2024.06.09 |
| [논문 리뷰] GaussianPro (arXiv2024) : surface 퀄리티 향상 (2) | 2024.06.07 |




댓글