본 글에서는 3D Gaussian의 설명과 함께 3D Gaussian을 World 좌표계에서 Image 좌표계(=Camera좌표계에서 거리가 1인 이미지 plane)으로 projection하는 방법을 다룹니다. NeRF(Neural Radiance Field)연구에서 큰 획을 그은 3D Gaussian Splatting논문을 이해하고자 정리하게 됬습니다.
본글에서는 EWA volume splatting(2001년) 논문에 적힌 개념을 설명하겠습니다. 선행 대수를 사용한 수식만 전개하므로, 이번글은 지루 할 수 있습니다. 수학에 자신있는 편이 아니라... 문제가 되는 부분이 있다면 지적 부탁드립니다.
3D Gaussain
3D Gaussian의 기본 개념부터 정리해보겠습니다.
1D / 2D / 3D Gaussian은 아래와 같은 형태를 가집니다. (그림 출처 : 1D link, 2D link, 3D link )
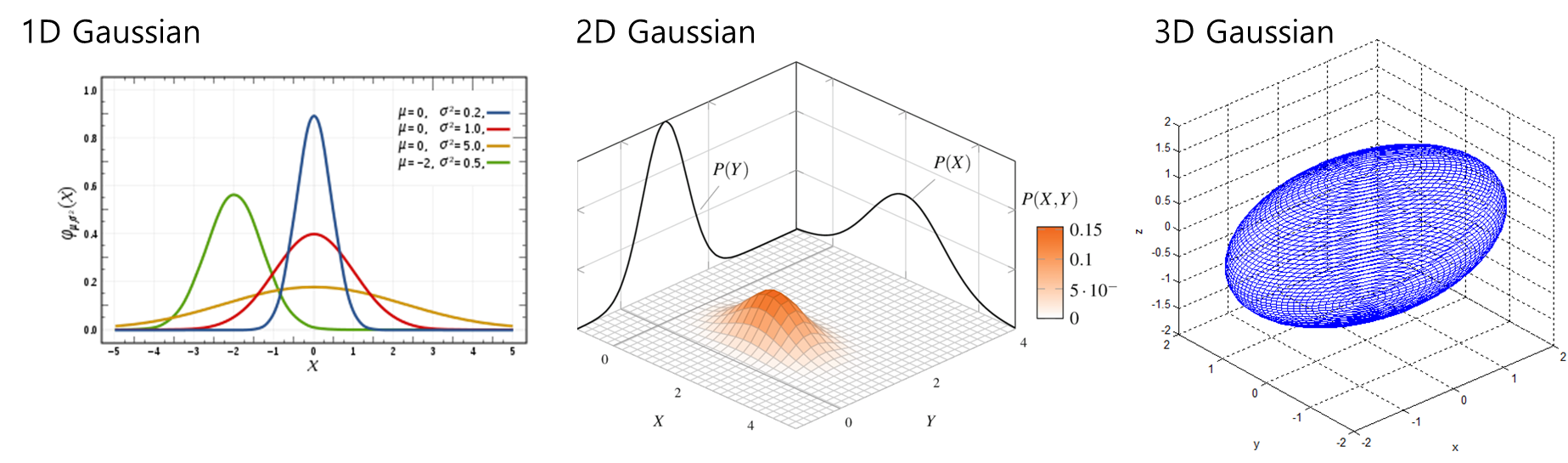
1-Dimension Gaussian의 pdf(probability density functions)수식 입니다. σ는 분산(variance)이고, μ는 평균입니다.

k-Dimension Gaussian의 pdf수식 입니다. Σ는 2개 차원을 쓰기 때문에 분산이 아니고 공분산(covariance)입니다.
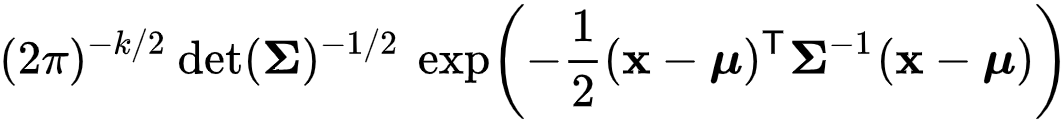
Det는 행렬식(determinant) 입니다.

3D Gaussian to 2D Projection
공분산 Projection 수식을 먼저보겠습니다. World좌표계에서 공분산Σ는 Image 좌표계의 covariance matrix Σ'로 아래 수식에 의해 계산됩니다. (좌표계에 대한 설명은 Camera Intrinsic/Extrinsic 개념 참고 바랍니다.)
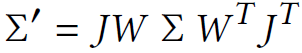
- Projective Transformation(Camera좌표계 -> Image 좌표계 변환 matrix)의 Jacobian(각 축으로 편미분한 Matrix) J
- Viewing Transformation (World좌표계 -> Camera 좌표계 변환 matrix) W
- World좌표계에서의 Covariance Matrix Σ
하나씩 뜯어보겠습니다.
World좌표계에서 Camera좌표계로 변환은 W*Σ*WT에 해당합니다. W의 Transpose형태가 뒤쪽에 붙는 이유는 Covariance 특성 때문입니다. (출처 : link )

J에 대한 이해를 위해, EWA volume splatting(2001년) 논문을 살펴보겠습니다.
3차원에서 2차원으로 projection될 때 함수는 비선형입니다. 그 이유는, World 좌표계에서 Camera 좌표계로 변환은 선형 변환이지만, camera 좌표계(아래 첫번째 그림)에서 직선 ray에 위의 point들은 image 좌표계(아래 두번째 그림)에서 비선형적인 것을 볼 수 있습니다.
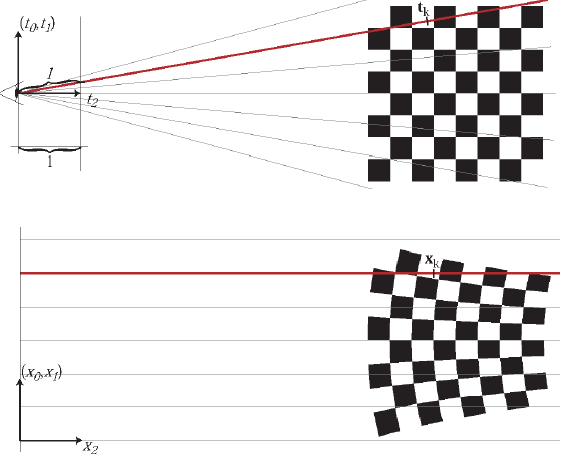
수식으로 보면, camera 좌표계 내 point t를 image 좌표계(camera좌표계에서 z축에 해당되는 t2가 1인 평면) 내 x로 mapping하는 함수를 Φ라고 할 때, 아래와 같이 정의되며, 이러한 형태는 Affine 변환(Ax+b형태의 선형 변환)이 불가능 한 것을 볼 수 있습니다.

비선형 변환을 선형 변환으로 만들어 주기 위해 Taylor Expansion개념이 사용됩니다. 기본 개념을 짧게 소개하자면 Taylor Expansion은 극소 지점(x=a)에서 여러 차수의 미분계수들로 구성된 다항 함수식입니다. (출처 : link )
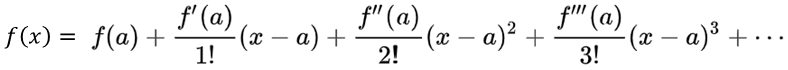
선형 변환으로 만들어주기 위해, point t를 테일러 전개(Taylor Expansion)를 사용하여 1차식으로 나타내면 아래 수식과 같습니다.
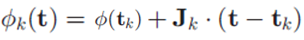
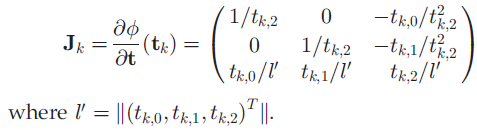
이는 Affine Transform이 아닌 Local Affine Approximation에 해당됩니다. Camera좌표계 내에서 임의의 좌표 tk주변에 존재하는 입력 좌표 t에 대해서는 Image좌표계로 선형 변환이 충족됩니다. 논문에서는 tk를 Gaussian의 중심점으로 지정하고 있습니다.

스크롤이 내려와서 다시 수식을 첨부하겠습니다. World 좌표계에서 covariance Σ는 Camera 좌표계로 변환할 때, 모든 voxel 좌표에 대해서 affine 함수를 사용하지만, Camera 좌표계에서 Image 좌표계로 변환 되는 covariance Σ'는 Jacobian값이 사용되어 집니다. 수식을 통해 정리하자면,
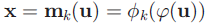
mk는 world좌표계의 u에서 image좌표계 x로 local affine approximation하는 함수
Φ(대문자-phi)는 camera좌표계 t에서 image좌표계 x로 local affine approximation 하는 함수

φ(소문자-phi)는 world좌표계 u에서 camera좌표계 t로 affine transformation하는 함수

위 3가지 수식을 조합하면, 아래 수식으로 만들 수 있습니다.

Covariance는 서로 다른 랜덤 변수의 상관관계를 나타내는 matrix이기 때문에 상수부분을 제외하면 x = J*W*u 이 되는 것을 볼 수 있습니다. (<- 이 부분은 확실하지 않습니다.)
위에서 언급한 Covariance 특성에 의해, J*W에 대한 Transpose를 뒤에 붙여주면, World 좌표계에서 covariance Σ를 Image 좌표계에서 covariance Σ'으로 변환하는 최종적인 공식은 Σ' = J*W*Σ*WT*JT이 됩니다.

간단하게 설명하기 위해 증명을 축약하였으며, 실제로 논문에서는 증명하는 방법이 조금 다릅니다. 증명 방법에 대해 부족하다고 느낀다면, 위의 내용들을 바탕으로 논문을 추가 참조바랍니다. 논문에서는 수식 (21)과 (30)이 같은 형태를 보이는 것을 볼 수 있으며, World 좌표계에서 Image 좌표계로 변환되는 함수 M은 W와 J의 곱형태로 나타나기 떄문에, J*W*Σ수식이 성립한다고 설명되어 있습니다.
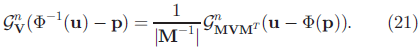

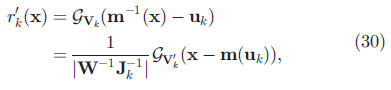
Covariance Dimension Reduction
Σ'는 3차원의 covariance값을 계산하므로 실제적으로 3x3 matrix가 되게 되는데, EWA volume splatting(2001년)논문에서 3차원 가우시안을 한쪽 축으로 적분하면 2차원 가우시안과 동일한 값을 가지게 되기 때문에 3번째 행과 열을 값을 버릴 수 있다고 합니다. g3은 3D Gaussian을 G2는 2D Gaussian을 나타내고, ^가 붙은 변수는 3D와 2D를 구분하기 위한 기호입니다.

때문에 Σ'는 3x3 matrix 대신에 2x2 matrix를 사용해도 된다고 합니다.

'Camera Model' 카테고리의 다른 글
| [개념 정리] Essential Matrix와 Fundamental Matrix (4) | 2024.03.25 |
|---|---|
| [개념 정리] Epipolar Geometry (0) | 2024.03.24 |
| [개념 정리] Canonical Coordinates (1) | 2023.10.26 |
| [개념 정리] Camera Intrinsic/Extrinsic Parameters #2 (6) | 2022.11.06 |
| [개념 정리] Camera Intrinsic/Extrinsic Parameters #1 (5) | 2022.11.03 |




댓글