Mip-Splatting: Alias-free 3D Gaussian Splatting, Zehao Yu, CVPR 2024
Novel View Synthesis(NVS) 계열의 논문들은 공통적으로 Scene을 Zoom-In, Zoom-Out 할 경우 Aliasing 현상이 발생합니다. Mip-NeRF(이전글), Mip-NeRF360(이전글)에선 NeRF모델에서 나타나는 Aliasing에 대해서 다루었습니다. 본 논문에선 3D Gaussian Splatting 모델(이전글)에서 나타나는 Aliasing을 해결 방법에 관해 다루고 있습니다.
Aliasing 현상은 기본적으로 Train 이미지의 pixel단위로 학습을 하기 때문에, 카메라가 앞/뒤로 움직이는 경우 scale이 고려되지 못하기 때문에 발생합니다. 논문에서는 더 구체적으로 문제를 분석하고 정리하고 있습니다.
3DGS에서 Aliasing 원인

위 이미지로 모든 문제들을 설명하고 있습니다. 원글을 많이 풀어서 썼습니다.
(a)는 Original 3DGS의 모델링 방식입니다. 카메라의 Image plane은 5pixel로 구성되어 있고 3D Object는 파란색입니다. 카메라에서 일정 거리에 있는 3D Object를 3D Gaussian으로 모델링할 경우, 검정색 선으로 만들어질 수 있습니다. 이를 Image Plane으로 projection하면 실제론 검정색선과 같은 2D Gaussian이지만, 빨간색 선과 같이 1개 Pixel을 꽉 채운 Dilated(팽창) 된 2D Gaussian으로 만들어지면서 pixel을 구성합니다. (논문 2번째장 3번째 문장에 original 3DGS가 low-pass filter를 사용해서 2D dilation operation이 적용된다고 되어 있습니다. original 3DGS 논문에는 유추할만한 내용이 없고 본 논문의 저자가 분석한 것으로 보입니다.)
(b)는 극단적인 경우를 가정합니다. 3D Gaussian의 분산이 아주 작은 값으로 셋팅되어 화살표처럼 실선이 되더라도, Image Plane으로 projection되면, (a)와 동일한 Dilated 2D Gaussian이 만들어지게 되고, 랜더링 결과도 동일합니다. 2D pixel으로 3D Gaussian을 구성할 때, 3D Gaussian scale에 constraint가 적용되지 않는다고 볼 수 있습니다.
(d)는 Zoom-in이 될 때 발생하는 문제를 보여줍니다. Zoom-in이 되면 카메라 focal length가 커지게 되고, 이는 World 좌표계에서 pixel의 size를 작게 만듭니다. 실제적으로 3D Object는 3개 pixel에 걸쳐서 표현되어야 하는데, 3DGS모델은 Scale을 고려하지 못하기 때문에 1개 Pixel로만 표현되고, 이는 Erosion(침식)의 형태로 랜더링하게 됩니다. 원래 사물보다 얇게 랜더링되기도 하고, 3D Gaussian이 얇게 표현됨으로써 high frequency artifact가 발생합니다.
(c)는 Zoom-out시의 문제점입니다. focal length가 줄어들면서 World 좌표계에서 1개 pixel이 커버하는 영역이 넓어지게 되고, Dilated 2D Gaussian(빨간색 선)이 실제 3D Object 크기 이상으로 형성됩니다. 때문에 Dilation(팽창) 형태로 랜더링되어 얇은 물체가 두껍게 표현되게 되기도 하고, 여러개의 얇은 Gaussian이 원래크기 보다 더 큰 크기로 projection되면서 빛이 양이 그만큼 많이 누적되어 밝게 표현됩니다. 이를 논문에선 brightness & dilation artifact가 발생하다고 표현하고 있습니다.
이 문제를 해결하기 위해서 단순히 Dilation을 사용하지 않게 되면, 너무 작은 3D Gaussian들이 랜더링 될 수가 없고, 학습 과정에서도 보이지 않는 아주 작은 3D Gaussian이 많이 만들어지게 되어서 GPU 메모리 문제도 발생하게 됩니다. 또한 이러한 것들을 무시하면서 dilation 없이 학습하더라도, Zoom Out시 artifact가 발생합니다.
저자는 Zoom-In을 해결하기 위해 3D Smoothing Filter를, Zoom-Out을 해결하기 위해 2D Mip Filter 기법을 제안합니다.
3D Smoothing Filter
Zoom-in시 aliasing을 해결하기 위해, 3D Gaussian를 샘플링하는 단위를 제한합니다.
논문에서는 학습이미지의 sampling rate 최대값으로 3D scene의 frequency를 제한한다고 나와있습니다. 알 수 없는 용어가 두개 나왔는데요. 아래 그림으로 설명하겠습니다.

T는 sampling interval입니다. 3D world좌표계에서 3D Gaussian을 샘플링하는 최소 간격으로 보면됩니다. 이 값은 3D Gaussian의 중심좌표와 카메라 중심 사이의 거리인 d와 카메라 focal length로 계산 할 수 있습니다. frequency는 발생 빈도로 해석 할 수 있는데요. 여기서 sampling frequency v는 T의 역수입니다. 단위 구간당 발생 빈도로 볼 수 있겠습니다. 또한 sampling frequency와 sampling rate는 동일한 용어입니다.

논문에서는 sampling frequency를 3D Gaussian(=primitive)마다 다르게 적용하고 있으며 각 3D Gaussian k에 대해 모든 학습이미지 N개들 중에서 가장 sampling frequency가 높은 값을 사용하게 됩니다.

모두 영상 신호처리에서 나온 용어라 생각됩니다. 다르게 쉽게 표현하면 위 그림인데요. sampling rate가 최대값을 가지는 건 sampling interval이 최소값을 가지게 되는것이므로, 학습이미지들 중에서 sampling interval이 가장 작은 값으로 결정됩니다. 위에선 camera 3이 되겠습니다.
Zoom-in시에 sampling interval을 최소 간격으로 만들기 위해서, 3D Gaussian에 Gaussian low-pass filter $g_low$를 씌워줍니다. 기존 3D Gaussian은 아래와 같으며,

low-pass filter를 제가 유추해보자면, (해당 수식은 논문에 없습니다.)
$$G_{\text{low}}(x) = e^{-\frac{1}{2} x^T \left( \frac{s}{\nu_k} I \right)^{-1} x}$$
논문에선 이를 합성곱해서 filtering한다고 되어 있습니다.

이를 전개하면,

s는 hyperparameter 상수값이며, $v_k$는 학습 과정중 m iteration마다 계산하게 됩니다. 논문의 Implementation파트에서 s는 0.2이고 m은 100이라고 나와있습니다. 이렇게 filter를 거치게 될 경우, 모든 Gaussian에 대해 가장 높은 frequency는 가장 높은 sampling rate의 절반을 초과할 수 없다는 것을 보장합니다. 논문 그대로 해석하면 와닿지가 않아서, 개인적으로 의미를 생각해보자면, 3D Gaussian의 가장 작은 크기는 해당 Gaussian에서 제일 가까이 위치하는 학습이미지 pixel크기에 의해 결정 된다고 보면 되지 않을까합니다. 위 필터링 수식은 너무 작은 Gaussian이 되지않도록 $s/v_k$만큼 더해줘서 dilation되는 효과를 주는 것으로 보입니다.
2D Mip Filter
Zoom-out를 처리해주기 위한 filter입니다. sampling rate가 너무 낮다면(=sampling interval이 너무 크다면) (c)와 같이 aliasing이 발생합니다.

이를 해결하기 위해, 이미지 표현시 주변 pixel값을 2D box filter를 사용해서 1개의 pixel을 추정하는 것과 같이, 아래 2D Mip Filter를 사용해서 1개의 pixel값을 추정합니다.
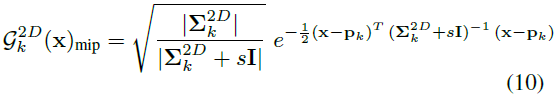
2D box filter를 대체한다고 되어 있기 때문에, 여러개 gaussian을 mip-filter를 통해서 1개의 gaussian으로 만들어준다고 볼 수 있을 것 같은데, 정확한 의미는 와닿지가 않네요. s는 상수값으로 0.1입니다.
Experiments
Blender 데이터셋을 해상도별로 학습한 결과입니다.

이미지를 1/2씩 줄여가면서, focal length를 2배씩 수정하면서 만든 데이터셋을 학습하고 평가했습니다. full resolution같은 경우 40% 샘플링했고, 다른 해상도는 20%샘플링해서 테스트했습니다. Aliasing을 평가하는 환경셋팅이 아님에도 높은 성능을 보입니다.
Blender 데이터셋으로 Zoom Out을 평가한 결과입니다.


full resolution으로 학습을 진행하고, 1/2, 1/4, 1/8 해상도로 평가를 진행했습니다.
Mip-NeRF360 데이터셋으로 Zoom In 을 평가한 결과입니다.


1/8해상도 데이터로 학습을 진행하고, full, 1/2, 1/4 , 1/8 해상도로 평가를 진행했습니다. 때문에 각각의 평가 결과는 표에서 역순으로 8x, 4x, 2x, 1x입니다.
Mip-NeRF 360데이터로 Scale을 동일하게 맞춘 실험입니다.

Zip-NeRF(이전글)이 가장 높은 성능을 보이지만, Aliasing을 다루는 Mip-Splatting도 높은 결과를 보이는 것을 볼 수 있습니다.
Limitation
문제점들을 나열하고 있습니다.
Zoom Out평가표에서 1/8res을 보면 Gaussian이 너무 작아지는 경우 문제가 되고 있습니다.
100 iteration마다 sampling rate를 계산하면서 학습 속도가 느려집니다.
Pytorch를 CUDA implementation을 효과적으로 바꾸면 성능 개선이 가능합니다.
sampling rate를 계산할 때 자료구조를 바꾸면 성능개선이 가능합니다.
Closing..
CVPR2024 best student paper라서 읽게 되었습니다. 결과물을 보고 왜 best paper인지 납득이 됬는데, 생략된 설명부분이 많아서 이해하기가 특히나 어렵네요. 이번글에선 잘못 리뷰한 부분이 꽤 있을꺼라 생각하고 있습니다. 저와 다르게 이해한 부분이 있다면 댓글 부탁드리겠습니다.
'3D-GS' 카테고리의 다른 글
| [논문 리뷰] Scaffold-GS (CVPR 2024) : MLP기반 3DGS (5) | 2024.08.25 |
|---|---|
| [논문 리뷰] Grendel-GS (arXiv2024) : Multi GPU로 3DGS (0) | 2024.08.10 |
| [논문 리뷰] PhysGaussian (CVPR 2024) : 물리 기반 변형 (3) | 2024.07.13 |
| [논문 리뷰] VastGaussian (CVPR 2024) : Large Scene (0) | 2024.06.17 |
| [논문 리뷰] GaussianEditor (CVPR2024) : 3D inpainting 연구 (2) | 2024.06.09 |




댓글