Epipolar Geometry개념(이전글)에 추가적으로 심화된 내용을 다루고자합니다.
Essential Matrix와 수식 유도과정
p에서 p'로 이동하는 변환 matrix를 Essential Matrix E라고 합니다.

위 수식은 Epipolar Geometry의 constraint 중에 하나이며, Essential Matrix의 개념을 파악하는데 중요하므로 수식 유도 과정을 설명하고자 합니다.
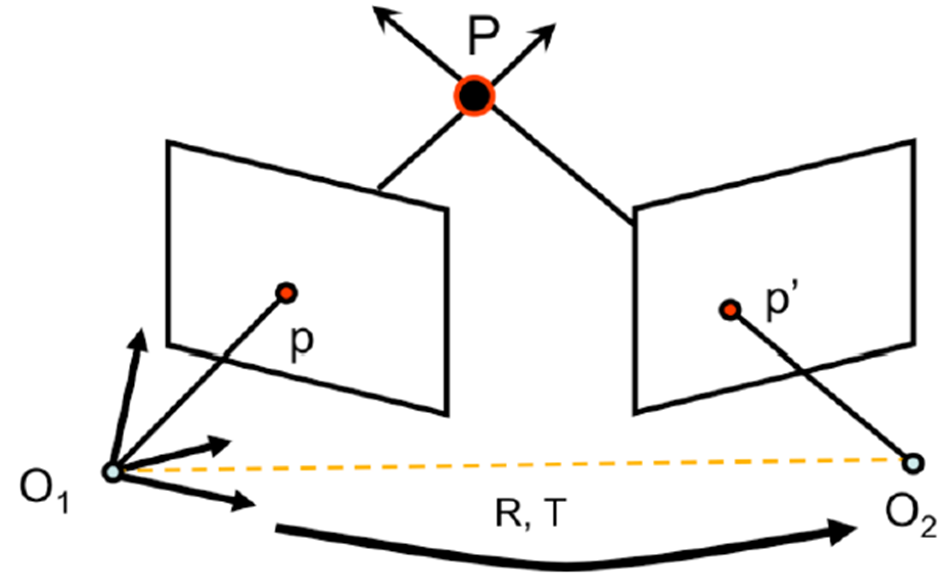
O_1을 원점으로 두었을 때, 2D p'의 3D위치는 Rp'+T입니다. O_1에서 Rp'+T로 향하는 vector는 O_1에서T로 향하는 vector와 epipolar plane에 위치하게 됩니다. 때문에 epipolar plane에 수직인 vector (=normal vector)는 Rp'+T vector와 T vector에 대한 외적(=cross product=X기호)으로 계산 할 수 있으며, T와T의 cross product는 0이므로 아래와 같이 간결하게 만들 수 있습니다.
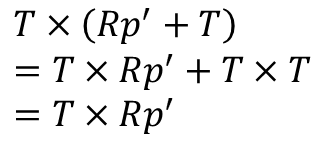
O_1에서 p로 향하는 vector p와 조금 전에 언급한 vector TxRp'는 수직인 관계에 있으므로, 2개 vector의 내적(=dot product =·기호)는 0이 됩니다.

3x1크기인 vector 2개의 외적(=cross product)를 행렬곱(=matrix multiplication)으로 표현하면, 아래와 같이 Matrix-vector간의 multiplication으로 나타낼 수 있습니다.

아래와 같이 외적(=cross product=X기호)가 행렬곱(=matrix multiplication)으로 표현되었습니다

그리고 p뒤에 내적(=dot product=·기호)는 1x3과 3x1의 내적이므로 행렬곱(=matrix multiplication)이 됩니다.
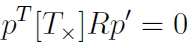
Essential Matrix E를 E=[Tx]R로 정의하면, 가장 처음에 언급했던 수식이 만들어집니다.

그 외 책에서 언급된 아래 수식에 대한 설명입니다.
Projection Matrix


점P가 left view의 점 p'로 projection되는 matrix M과, 점 P가 right view의 p'로 projection되는 matrix M'은 아래와 같습니다.

3D에서 2D로 Projection Matrix는일반적으로 아래와 같은 꼴입니다. intrinsic/extrinsic parameter 글 참고 바랍니다.

p와 p'의 관계성을 단순하게 보기 위해, intrinsic parameter는 단위행렬 I로 두고 extrinsic parameter인 R과 T만 고려합니다. left view의 O_1을 World좌표계의 원점으로 두고, O_1에서 O_2로 rotation하는 matrix를 R, translation하는 matrix를 T로 둔다면, M은 회전과 이동이 필요없으므로 단위행렬이 되고, O_2는 R만큼 회전하고 M'은 O_2가 O_1으로 이동한 후 R만큼 회전해야 하므로, extrinsic matrix의 4열로 존재하는 T자리에는 -RT가 들어갑니다.

Fundamental Matrix 수식 유도 과정
여기선 Fundamental Matrix가 어떻게 만들어지는지 소개합니다.
Fundamental Matrix엔 intrinsic parameter K가 고려됩니다.
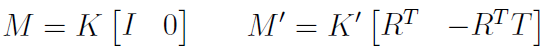
p와, p'에 intrinsic parameter가 고려됬을 경우 projection관계를 나타내면 아래 수식이 만들어지고,

앞선 Essential Matrix에서 언급된 수식에 p대신 pc를 넣고
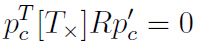
이를 풀어쓰면, 아래와 같이됩니다.

여기서 F를 아래 수식으로 정의하면,

최종적으로 아래 epipolar constraint수식이 만들어집니다.

Epipolar line 수식
Essential Matrix E에 p'를 행렬곱은 left view에서 epipolar line이게 됩니다.

epipolar line은 p가 존재 할 수 있는 후보 선이며, 위에서 증명했던 수식을 바탕으로

Ep'를 l로 바꾸면, p와 l의 내적이 되는데, p는 l위에 존재하므로, 0이 되는 것을 볼 수 있습니다. 때문에 반대 case도 가능합니다.

essential matrix E와 epipole e의 내적
그 외에, essential matrix E와 epipole e의 내적은 0이 된다는 특성이 있습니다.

epipole e'와 epipolar line l'의 내적은 0이되는데, 결합법칙을 통해, 0이 됨을 알 수 있습니다.
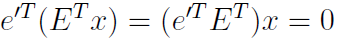
출처
'Camera Model' 카테고리의 다른 글
| [개념 정리] SfM(Structure from Motion) of COLMAP - 1부 (8) | 2024.05.03 |
|---|---|
| [논문 리뷰] DUSt3R (arXiv 2023) : Pose-free 3D Reconstruction (0) | 2024.04.22 |
| [개념 정리] Epipolar Geometry (0) | 2024.03.24 |
| [개념 정리] Canonical Coordinates (1) | 2023.10.26 |
| [개념 정리] 3D Gaussian 과 2D projection (3) | 2023.09.18 |




댓글