이전 포스트 에서는 Camera Parameter가 어디서 사용되는지와 Pinhole Camera Model, 4가지 Coordinate System에서 대해서 설명하였습니다. 본 포스트에서는 Camera Parameter를 수식적으로 설명합니다.
4가지 Coordinate System은 다음과 같이 표현 될 수 있습니다.
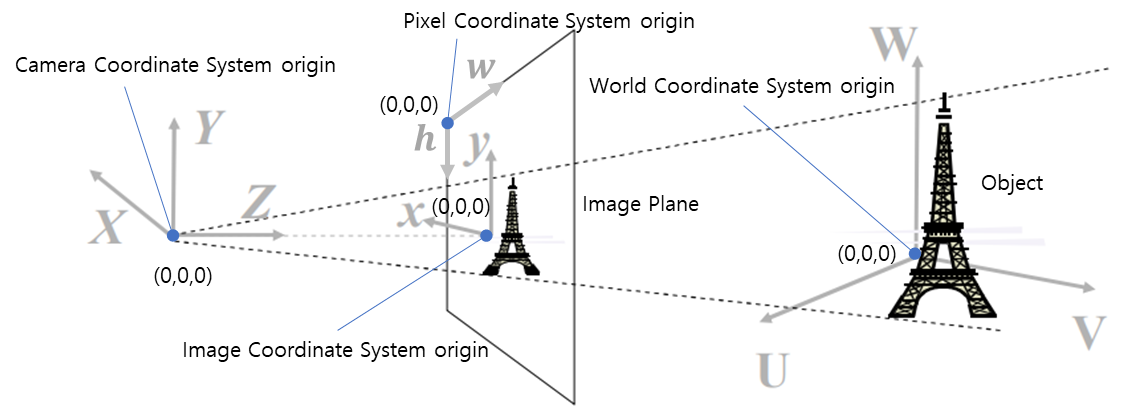
해당 좌표계들에 있는 점들은 행렬변환을 통해 서로 변환이 될 수 있습니다.
World Coordinate -> Camera Coordinate -> Image Coordinate -> Pixel Coordinate 로 변환이 가능하고, 역순으로도 가능합니다. World Coordinate를 Pixel Coordinate로 변환하는데 카메라에 대한 정보가 필요하게 되는데, 이 때 필요한 Parameter들을 Camera Parameter라고 하고 행렬P 로 표현됩니다.
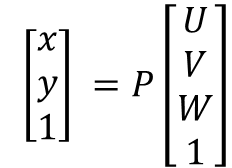
Camera Parameter의 행렬 연산을 통해, World Coordinate System(U,V,W)에 있는 voxel을 Image Coordinate System(x,y)로 변환할 수 있습니다.
P는 2개의 크게 2개의 Parameter로 구성됩니다.
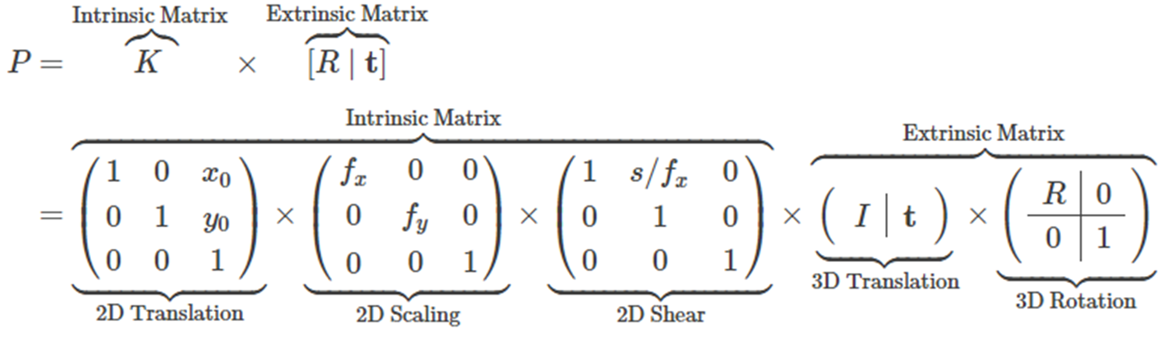
Extrinsic Parameter는 3D 공간 내에서 카메라가 어디에 위치(3D Translation)하고 있고, 어디를 바라보고 있는지(3D Rotation)에 대한 Parameter입니다.
Intrinsic Parameter는 카메라 렌즈와 센서 위치에 의해서 결정되어지는 항목으로써, 이미지 패널이 얼마나 이동(2D Translation)하고, 얼마나 확대하고(2D Scaling), 얼마나 기울어졌는지(2D Shear) 대한 Parameter입니다.
Intrinsic은 카메라 박스 내에서 조절하는 parameter를, Extrinsic은 그 외적인 parameter라고 생각하시면 됩니다.
Extrinsic Matrix는 4x4이고 Intrinsic Matrix는 3x3입니다. 그러면 곱셈이 불가능합니다. 이에 대해서는 뒤에서 언급드리겠습니다.
수식을 설명하기 앞서 Transformation Marix 기본을 살짝 언급하자면 아래와 같습니다. 3차원도 동일하게 적용됩니다. 2행만 수식에 사용되지만 행렬 연산을 위해서 정방행렬이 되어야 하기 때문에, [0, 0, 1]이 마지막 행에 붙습니다.

Extrinsic Matrix

World좌표계를 Camera좌표계로 변환하는 Matrix입니다. 왼쪽 행렬의 t는 World 좌표계에서 Camera 좌표계로 얼마나 이동 해야 하는지를 나타내는 Transition Vector이고, 오른쪽 행렬의 R은 Camera좌표계 안에서 World좌표계의 Axis(축) 방향을 나타내는 Rotation Matrix입니다. 이러한 Parameter는 일반적으로 Camera Pose를 통해서 산출됩니다. 위 행렬에 대한 역행렬은 Camera좌표계를 World좌표계로 변환하는 Matrix가 됩니다.

C는 World 좌표계 내에 카메라의 위치를 나타내고, Rc는 World좌표계의 Axis(축)을 기준으로 카메라의 방향을 나타냅니다. 단순하게 원점만 생각하면 t=-C 가 아닌가?라고 생각할 수 있는데, 축이 회전 되기 때문에 Rotation도 고려가 되어져야 됩니다. R은 Rc의 Transpose가 되고, t는 -R*C가 됩니다.
아래는 추가 이해를 위해 다른 출처에서 들고왔습니다. Parameter가 위와 다르게 표시되었습니다. c는 Camera에 관련된 Parameter고, w는 World 좌표계와 관련된 Parameter입니다.

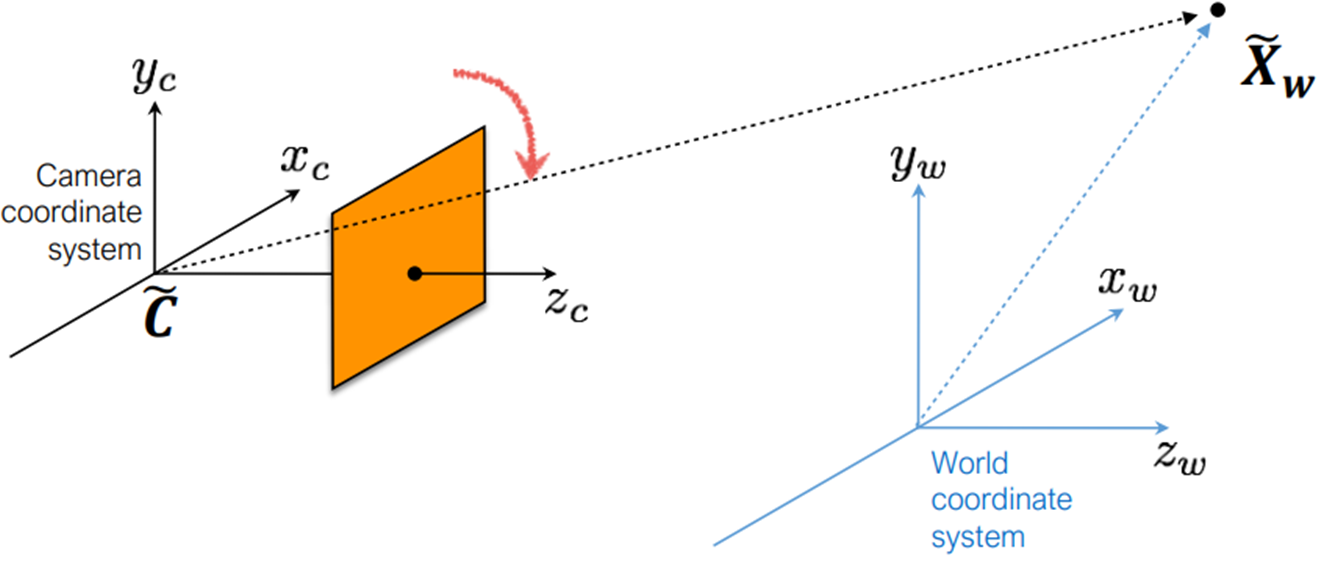
Xw라는 world 좌표계내의 점을 Camera좌표계로 이동하기 위해, World좌표계의 내에서 Camera좌표계의 Origin위치인 C만큼을 빼주고 (1번째 그림), 카메라 포즈 Rc Matrix를 Transpose한 Matrix(=R)로 회전합니다(2번째 그림).
WebGL로 공개된 github을 참고하여,각 인자 값을 변화해서 랜더링 해보면 다음과 같이 됩니다. https://ksimek.github.io/perspective_camera_toy.html

이번에는 C와 Rc가 아닌, t와 R로 표현되었습니다. World좌표계의 Origin이 Base사진 기준으로 Object 뒤쪽에 있을 거라 생각이 됩니다.
다음으로 Intrinsic Parameter를 보겠습니다.
Intrinsic Parameter

앞에서는 3D공간내의 카메라 Pose와 관련되었다면, Intrinsic Parameter는 Pinhole 카메라 위치가 고정된 상태에서, 카메라 Focal Length(fx, fy), Principal Point의 위치(x0,y0)를 변화시키는 내부 Parameter와 관련이 있습니다. Extrinsic Parameter를 통해, World좌표계에서 Camera좌표계로 변환이 됬다면, Intrinsic Parameter는 Camera 좌표계에서 Pixel 좌표계로 변환하는 것에 대한 것입니다. 2D Translation, 2D Scaling, 2D Shear Matrix로 구성되어 있고, 각 Matrix에 대해 다뤄보겠습니다.
2D Scaling Matrix
Focal Length는 3D 공간 내의 점을 2D Plane으로 Projection하기 위해 필요한 필요한 인자입니다. Focal Length에 따라, 3D point가 Image Plane내의 2D point로 확대 또는 축소되어 맵핑되어 집니다. 때문에 Focal Length는 Scaling에 대한 Parameter임을 알 수 있습니다.

Scaling에 대한 수식을 다시 보면, Z인자는 없습니다.

카메라 모델에서는 X,Y를 각각 Z로 나누어 Z가 1인 Normalized Plane으로 이동시키고, Focal Length값에 따라 크기 조정(Scaling)하는 형태가 됩니다. 때문에 Scaling Matrix가 위와 같이 만들어집니다. 초반에 언급드렸던, 위 수식으로는 Extrinsic Matrix와 Intrinsic Matrix가 곱해 질 수 없다고 했었습니다. 위 수식은 설명을 위한 수식이고, X,Y를 Z로 나누는 과정이 생략되었습니다.

3D좌표를 2D로 변환하는 수식이며, x,y는 2D 좌표, X,Y,Z는 3D좌표입니다. 3x4에 4x1 matrix가 곱해지면 3번째 값이 Z가 되는데, 좌측항에 1을 만들어주기 위해 Z를 나누주게 됩니다.
정리하자면, X,Y에 focal length가 곱해지고 Z로 나누면서, 3차원 좌표계가 2차원 좌표계로 변환이 됩니다. 이를 통해 카메라 위치가 좌표계의 원점인 Camera Coordinate System이 아닌 이미지 중심이 좌표계의 원점인 Image Coordinate System으로 변환이 됩니다.
2D Translation Matrix
Image Coordinate System을 Pixel Coordinate System으로 변환하는 것에 대해 다룹니다. 설명을 위해 먼저 Principal Point(주점)개념에 대해 다루겠습니다. 이전 포스트 에서 그래픽스의 Camera Model은 Pinhole Camera Model을 기반으로 사용된다고 했었습니다. 그리고 실제 이미지 판독 센서는 Pinhole 뒤에 위치해서 실제 이미지는 상하좌우반전이 발생하기 때문에, 이를 편의상 Pinhole 앞쪽에 Image Plane을 그려서 생각한다고 했었습니다. Principal Point를 설명하기 위해 Pinhole 뒤에 Image Plane을 위치시키겠습니다.

Principal Point는 Pinhole을 기준으로 수직으로 Ray를 그렸을 때, Image Plane의 중심을 의미합니다.
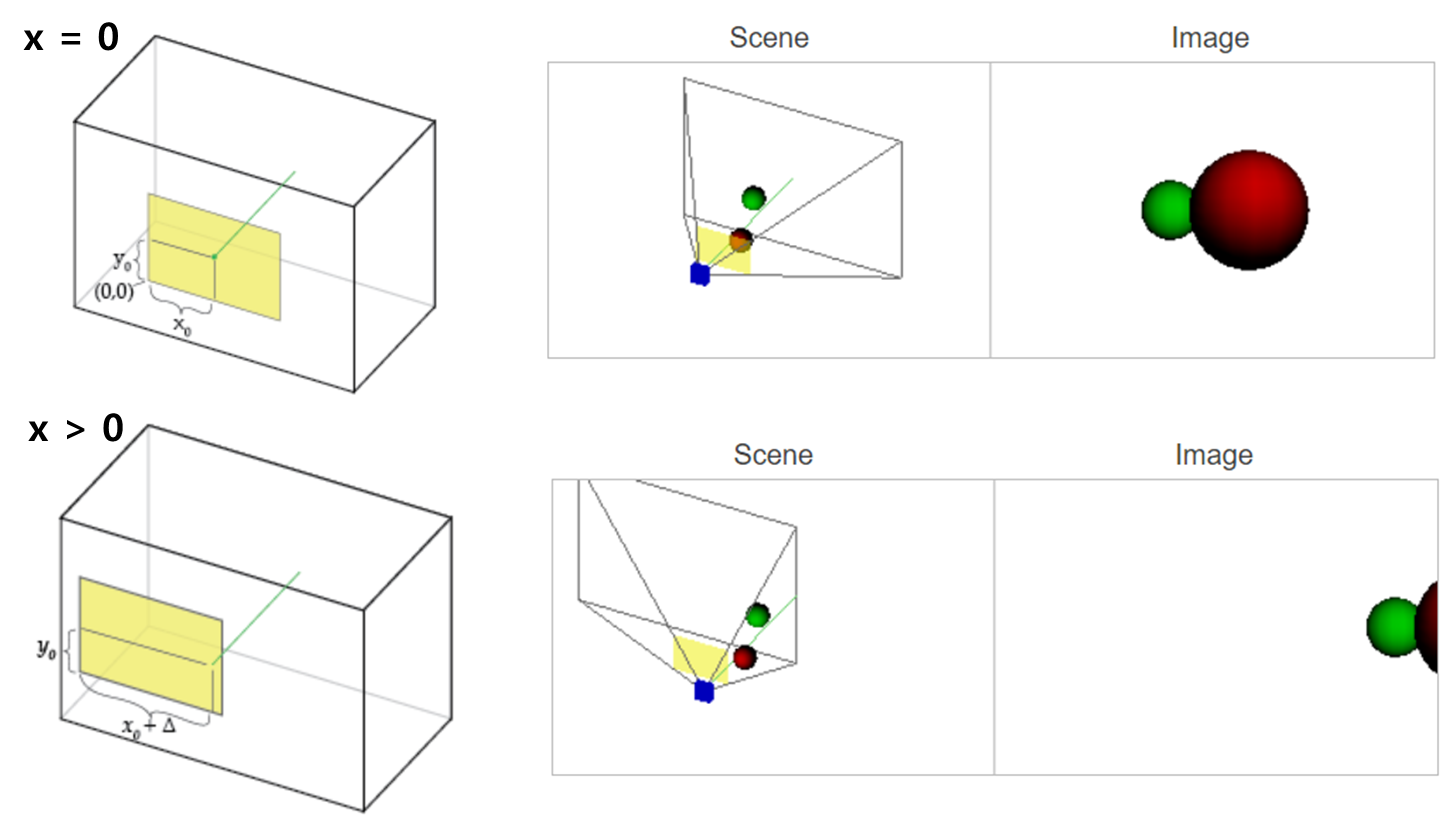
위 그림은 principal point가 중심인 경우와 x축으로 이동한 경우를 나타냅니다. Principal Point가 Image Plane의 중심이 아니게 되면, 카메라 정면의 물체를 프레임에 못담게 되는 이상한 현상을 볼 수 있습니다. 때문에 pinhole의 위치가 항상 중앙에 있다고 생각하면 될 것 같습니다. (아닌 경우가 있을지는 잘 모르겠네요.)
이제 Image Coordinate System을 Pixel Coordinate System로 바꾸는 2D Translation Matrix 설명 본론입니다.
Image Coordinate System은 좌표계의 원점이 Image Plane의 중심이 될 경우, Pixel Coordinate System은 좌상단 또는 좌하단을 원점으로 갖게 될 경우를 말합니다.
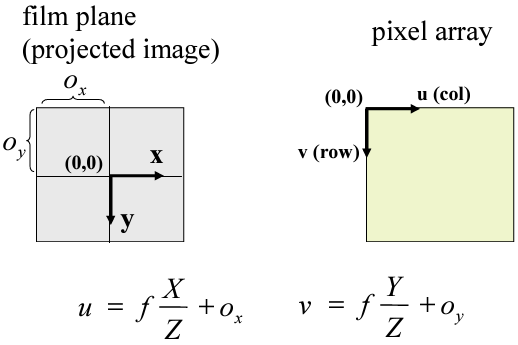
앞서 본 Principal Point을 기준으로 offset값을 주게되면 Image 좌표계에서 Pixel 좌표계로 변환이 됩니다. Translation Matrix를 통해 ox, oy만큼 이동이 가능합니다. 아래 수식에선 x0, y0에 해당됩니다.

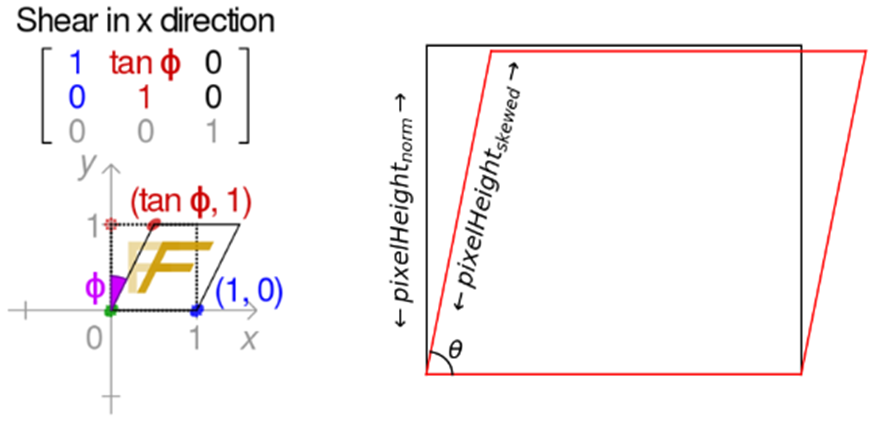
2D Shear Matrix
실제로 사용되지 않는 Parameter입니다. s는 Axis Skew를 나타내며, Scale값을 제거해 주기 위해, fx로 나누어지는 것으로 보입니다.
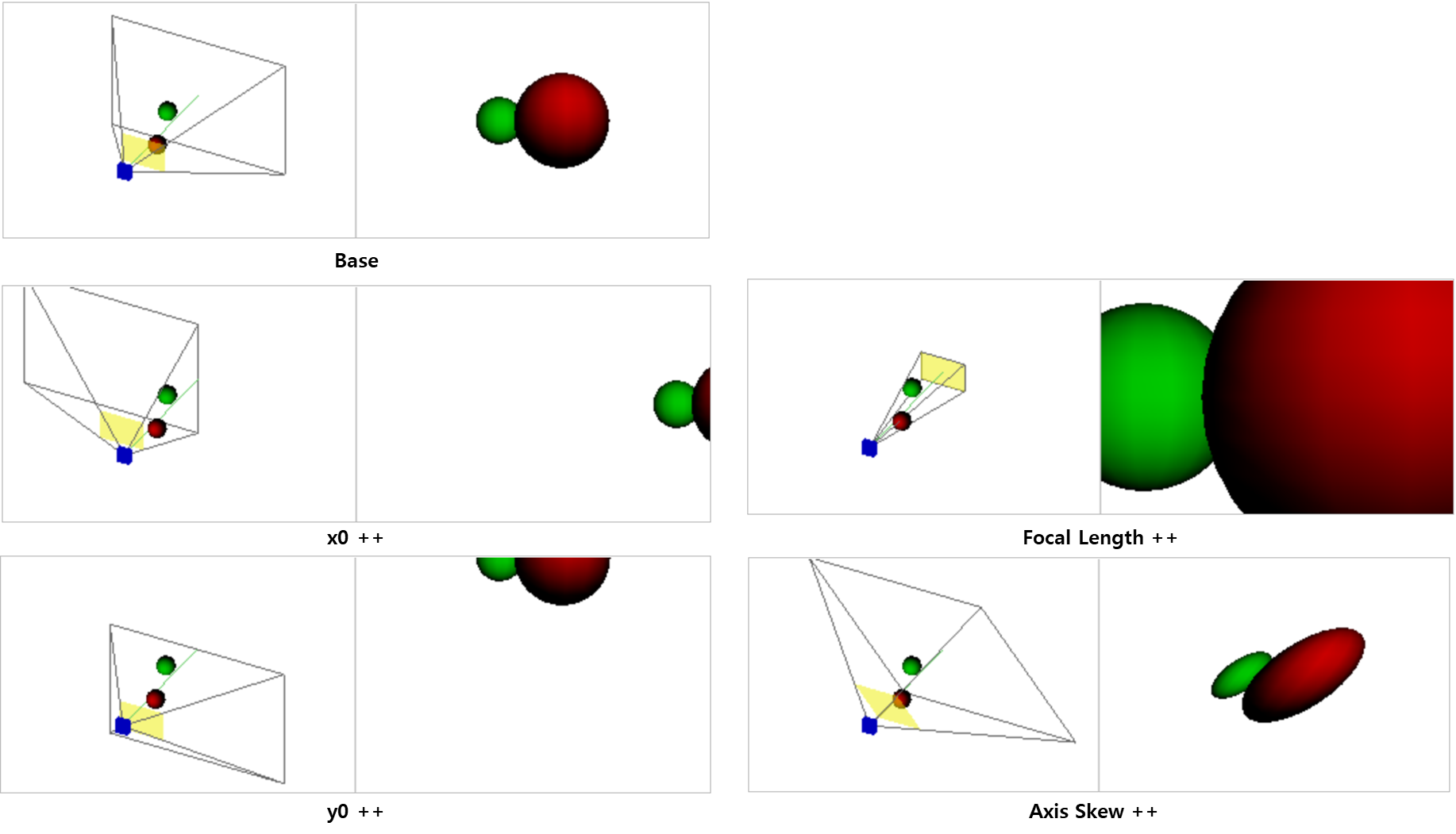
Parameter를 변경해서 보면 다음과 같습니다.
https://ksimek.github.io/perspective_camera_toy.html
Inverse Transform
World Coordinate -> Camera Coordinate -> Image Coordinate -> Pixel Coordinate 변환하는 방법에 대해 알아봤습니다. 반대 과정인 Pixel Coordinate -> Image Coordinate -> Camera Coordinate -> World Coordinate를 생각해보자면, Camera Coordinate -> World Coordinate에 대해서는 역함수를 통해 위에서 언급하였었습니다. Pixel Coordinate -> Camera Coordinate같은 경우에는 Z값이 소실되서 정확한 수치로 변환이 불가능하지만, 여러 카메라에서 획득한 상대적인 연산은 가능합니다.
Closing..
NeRF 라는 연구를 알아보다가, 카메라 모델과 관련된 이론과 코드가 많이 언급되어서 Camera Parameter를 정리 해봤습니다. 데이터셋을 만드는데 이론이 안잡혀 있으면, 카메라가 어디를 바라보는지 종잡을 수가 없더군요. 본 글이 NeRF뿐만 아니라 여러 분야에서 많이 참고 되었으면 합니다.
출처
https://ksimek.github.io/2013/08/13/intrinsic/
https://ksimek.github.io/2012/08/22/extrinsic/
http://www.cs.cmu.edu/~16385/lectures/lecture10.pdf
https://www.cse.psu.edu/~rtc12/CSE486/lecture12.pdf
https://www.cse.psu.edu/~rtc12/CSE486/lecture13.pdf
https://blog.immenselyhappy.com/post/camera-axis-skew/
'Camera Model' 카테고리의 다른 글
| [개념 정리] Essential Matrix와 Fundamental Matrix (4) | 2024.03.25 |
|---|---|
| [개념 정리] Epipolar Geometry (0) | 2024.03.24 |
| [개념 정리] Canonical Coordinates (1) | 2023.10.26 |
| [개념 정리] 3D Gaussian 과 2D projection (3) | 2023.09.18 |
| [개념 정리] Camera Intrinsic/Extrinsic Parameters #1 (5) | 2022.11.03 |




댓글