Epipolar Geometry는 1개의 3D Point, 2개의 카메라, 이미지 plane간의 관계를 나타내는 Geometry입니다.
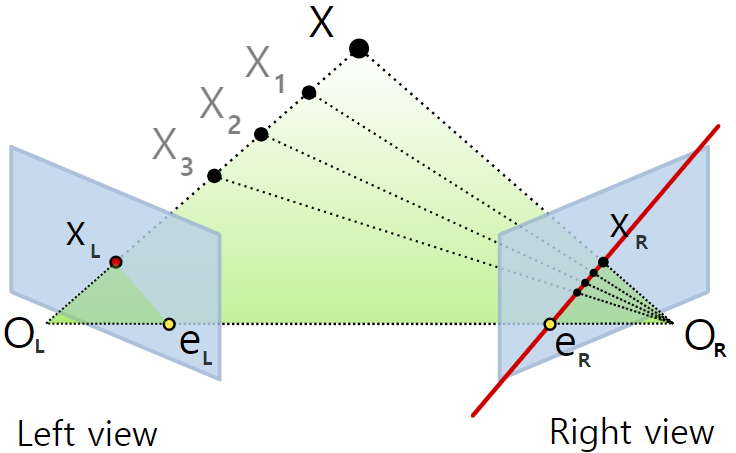
위 그림은 2개의 카메라 원점(OL, OR)에서 촬영된 이미지(파란색평면) 내 점(XL, XR)과 3차원 점(X)간의 관계를 표현하는 그림입니다. Epipolar Geometry를 파악한다면 다양한 문제를 풀 수 있습니다.
left view에서 한개의 점(XL)을 기준으로 조건에 따라 알 수 없는 변수 값은 아래와 같으며, 이 중에 몇개가 주어진다면 다른 값들을 추정 할 수 있습니다.
- 3차원에서의 XL의 위치 : X
- 다른 view에서 동일점 위치 : XR
- Camera Extrinsic Parameter (이전글 참고)
- camera position
- camera rotation - Camera Intrinsic Parameter (이전글 참고)
- focal length (= scale)
- principal points
- shear
예를 들자면,
- 예시1) 2개 이미지 내 동일 점의 위치, 카메라 intrinsic/extrinsic prameter를 알면 3D Point의 좌표를 계산 할 수 있습니다.
- 예시2) 2개 카메라 intrinsic/extrinsic parameter가 주어진다면, left view에서 점XL은 right view의 XR~eR를 잇는 선위에 위치하게 됩니다. left view에서 XL의 깊이를 알 수 없기 때문입니다. XR~eR을 잇는 선을 epipolar lines이라고 부릅니다.
- 예시3) 2개 이미지 내 동일점의 위치 8개만 주어지면, 2개 이미지간의 변환관계 matrix를 계산 할 수 있습니다.
이러한 맥락으로 epipolar geometry를 이해하면, scene의 3D structure를 알지 못하더라도 2개 이미지간 관계에 대한 constraint를 만들 수 있게 합니다. 이러한 constraint는 다른 값들을 추정하는데 쓰이게 됩니다.
용어
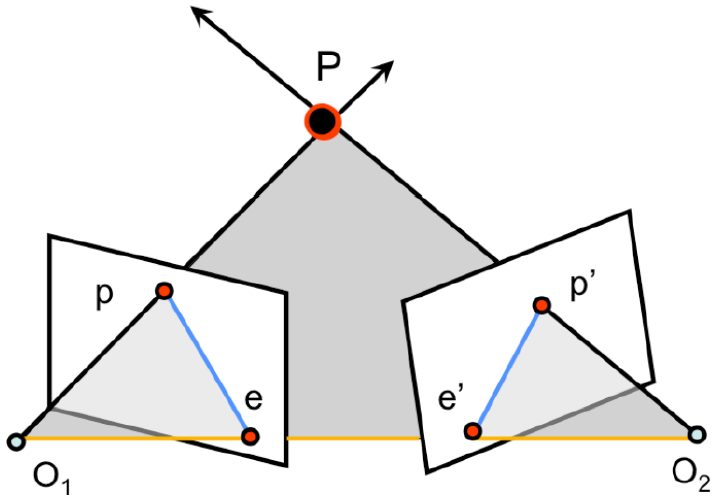
Epipolar Geometry에 사용되는 용어를 먼저 정리해보겠습니다. 위 그림은 3D point P를 관측하는 2개 카메라의 image plane을 나타내는 표준셋팅을 보여줍니다.
- baseline : 카메라 중심점 O1, O2를 잇는 선 (주황색)
- epipolar plane : 카메라 중심점 O1, O2와 3차원 point 좌표 P를 잇는 평면 (회색면)
- epipole : Image plane과 baseline가 교차하는 점 (e와 e')
- projection of points : 3차원 point좌표가 Image plane으로 투영된 점 (p와 p')
- epipolar lines : epipolar plane과 image plane이 교차하는 선 (e-p와 e'-p', 예제2에서 언급한 선, 파란색선)
한번 읽어서는 파악되지 않을 거라 생각됩니다. epipole과 epipolar line는 아래에서 많이 언급될 예정이므로, 한번 더 보고 넘어가시길 바랍니다.
다음으로 자세한 설명이 필요한 2가지 용어에 대해 보겠습니다.
Essential Matrix

Essential Matrix E는 left view의 p와 행렬곱(matrix multiplication)으로 right view의 p'좌표로 변환시키는 matrix를 말합니다. 특히 camera intrinsic parameter를 고려되지 않는 경우(= intrinsic parameter가 단위행렬)를 가정하고 있습니다. Essential Matrix를 찾게 되면, 3차원 P위치를 모르거나 camera parameter가 주어지지 않는 상황에서 다른 view에서 epipolar line을 찾는데 쓰이게 됩니다. Essential Matrix를 알고 있을 경우, 아래 수식을 통해 right view의 p'가 될 수 있는 위치인 epipolar line을 계산 할 수 있습니다. E는 Essential Matrix입니다.
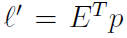
위 수식은 아래 수식으로 파생된 식이며, Epipolar Constraint수식 중에 하나입니다.
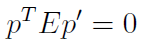
위 수식에 대한 유도과정은 Essential Matrix와 Fundamental Matrix글로 정리해두었습니다. Essential Matrix 계산 방법은 아래에서 다루겠습니다.
Fundamental Matrix
Fundamental Matrix는 Essential Matrix에서 카메라 intrinsic parameter(=K matrix)를 모두 같이 고려하는 matrix입니다. 다른 말로하면 focal length가 1이 아닌 경우(=scale이 바뀌는 경우)가 고려되어지는 matrix입니다.
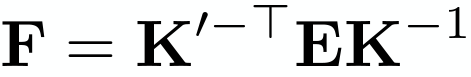
left camera의 intrinsic parameter인 K와 right camera의 intrinsic parameter인 K'가 앞뒤로 곱해지는 형태입니다.

Fundamental Matrix는 Essential Matrix와 동일하게 다른 view에의 epipolar line을 찾을 때 사용 될 수 있습니다.
여기까지 Essential Matrix, Fundamental Matrix개념과 함께 이 값을 알게 될 경우에 활용처에 대해서만 설명했습니다. 다음으로 어떻게 이 Matrix를 계산하는가에 대해 다루겠습니다.
Camera parameters로 Fundamental Matrix 계산
실생활에선 획득하기 어려운 카메라 parameter정보들이 모두 주어지는 경우 쉽게 계산됩니다. 예를들면, 3D 시뮬레이터나 현실에서 카메라를 고정 각도로 셋팅한 환경 등에서만 가능합니다.
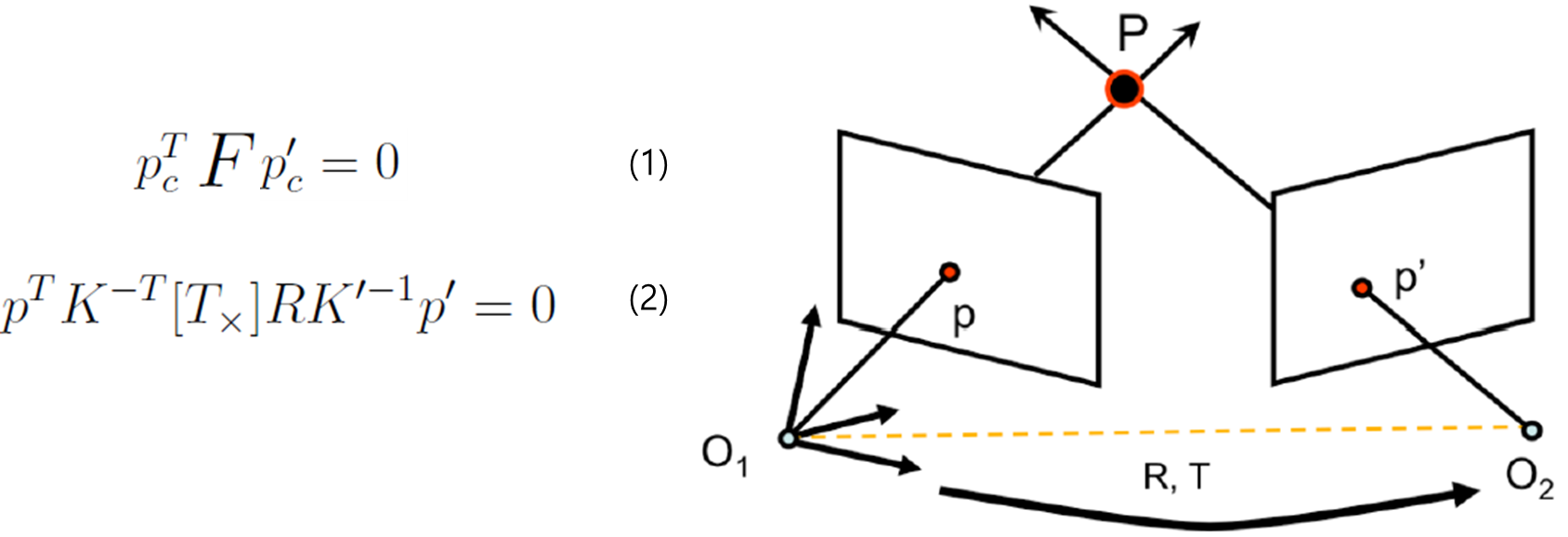
수식 유도과정 글을 참고하면, 수식1은 수식2로 나타내어집니다. 2개 카메라의 intrinsic parameter K, K', 2개 카메라 extrinsic parameter로부터 left camera에서 right camera로의 변환 rotation matrix R, translation T를 알면 Fundamental Matrix F를 matrix multiplication을 통해 쉽게 계산 할 수 있습니다.
Eight-Point Algorithm
camera parameter가 주어지지 않고 2개의 이미지와 대응점(corresponding points) 8개 pair를 위와 같이 주어질 경우 fundamental matrix를 계산하는 알고리즘입니다. 8개 pair point는 Image Matching 알고리즘으로 추출한다는 전제가 있는 것으로 생각되어집니다.
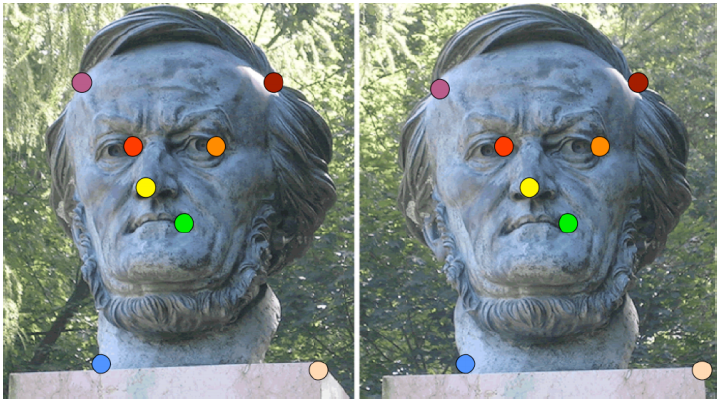
Fundametal Matrix정의에서 언급된 수식에다가, p와 p'가 8개 pair로 주어질 때, F matrix를 계산하는 형태입니다.
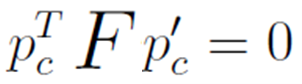
F는 3x3개로 구성되어 있으므로 9개의 미지수를 갖게 되며, p,p'쌍이 8개이므로 8개의 방정식을 만들 수 있습니다. 이 8개 연립방정식의 해를 찾으면 F를 계산 할 수 있습니다. pFp'식을 풀어서 계산하여 만들어진 방정식을 행렬로 표현하면 아래와 같습니다. (p는 좌표 u,v로 구성되며, p'는 좌표 u',v'로 구성됨)
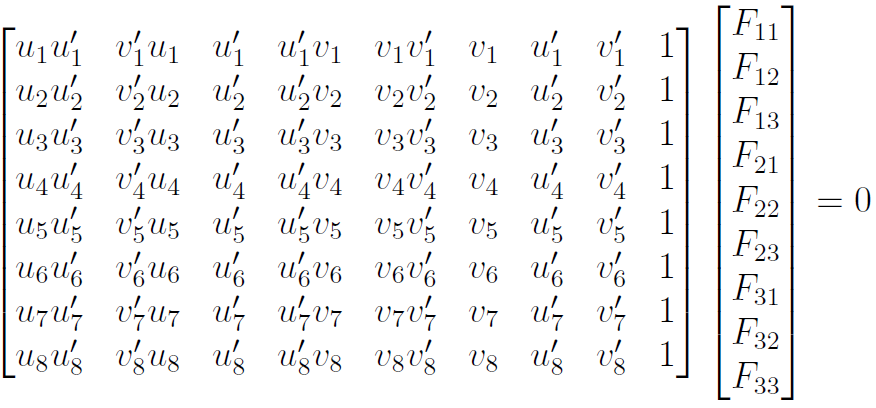
9개의 미지수를 가진 8개 방정식으로 해(=F)를 찾기 위해, SVD(Singular Value Decomposition:특이값 분해)를 사용해서 근사값을 찾을 수 있다고 합니다. p와 p' 쌍의 갯수 적을수록 오차가 많아지고, 많이 주어질수록 정확한 값을 계산 할 수 있다고 합니다.
추가적으로 p,p'쌍을 8개로 유지하면서 오차를 줄일 수 있는 방법으로 p와p'를 normalization하는 Normalized Eight-Point Algorithm이 있습니다.
Image Rectification
2개의 이미지를 평행 이동 관계로 만드는 것을 Image Rectification이라고 합니다.

eight point알고리즘으로 p,p'에 대한 epipolar line(좌하단 이미지의 파란색선)을 찾을 수 있으며, 이 epipolar line들을 바탕으로 2개 이미지를 평행하게 만드는 변환 matrix H를 찾을 수 있습니다.
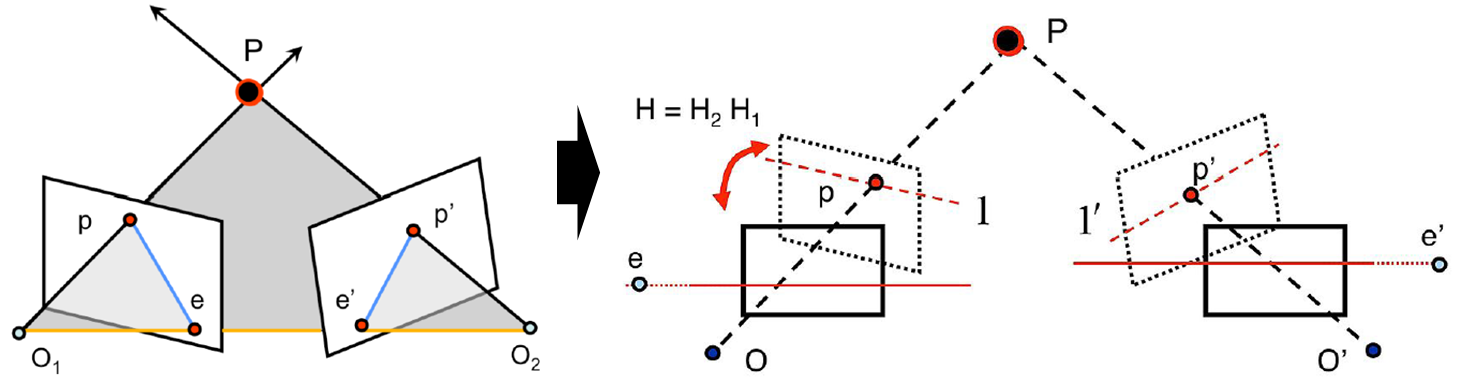
위 문제 또한 SVD를 사용하며, 아직 개념을 정확히 이해하지 못해서 이해된다면 자세한 내용을 다른 별도의 글로 다뤄보겠습니다.
출처
https://web.stanford.edu/class/cs231a/course_notes.html
'Camera Model' 카테고리의 다른 글
| [논문 리뷰] DUSt3R (arXiv 2023) : Pose-free 3D Reconstruction (0) | 2024.04.22 |
|---|---|
| [개념 정리] Essential Matrix와 Fundamental Matrix (4) | 2024.03.25 |
| [개념 정리] Canonical Coordinates (1) | 2023.10.26 |
| [개념 정리] 3D Gaussian 과 2D projection (3) | 2023.09.18 |
| [개념 정리] Camera Intrinsic/Extrinsic Parameters #2 (6) | 2022.11.06 |




댓글