DREAMFUSION: TEXT-TO-3D USING 2D DIFFUSION, Ben Poole, arXiv2022, Google Resarch
SDS(Score Distillation Sampling) Loss는 Diffusion Model 기반의 Score Loss이며, Google Research에서 연구한 DreamFusion (ICLR 2023) 에서 처음 언급되었습니다. Text-to-3D 모델을 생성 할 때 사용되는 Loss입니다.
짧게 요약하자면, 3D를 랜더링한 이미지가 2D Diffusion model에 condition(=text 등)을 입력으로 생성된 이미지와 다를 경우 커지도록 설계된 Loss입니다.
기본 개념
Diffusion Model (이전글)을 참고하여 설명하자면, NeRF(또는 Gaussian Splatting)으로 랜더링한 이미지는 가장 오른쪽 이미지 XT에 해당하고, Xt에서 X0로 Reverse Diffusion Process를 진행하면서 이미지가 생성이 되게 됩니다. xt 이미지가 U-Net을 통과하면 Diffusion 모델 학습시 xt-1에서 사용된 Image와 유사한 확률분포를 가진 이미지를 생성하게 됩니다.

이제 아래 그림 Stable Diffusion을 보겠습니다. Image 또는 Text를 임베딩한 값(τθ)을 UNet의 입력으로 넣어주면, 임베딩한 값과 유사한 style을 가지면서, 2D diffusion prior학습시 사용된 이미지와 유사한 확률분포를 가진 이미지를 생성하게 됩니다.

U-Net이 고정된 상태에서, NeRF로 생성한 값(Zt)와 임베딩값(τθ)을 입력으로 U-Net을 통과해서 생성된 결과값이 2D diffusion prior학습시 사용된 이미지의 확률분포와 유사하지 않을 경우 Loss가 커지게 설계되어, 그 차이가 NeRF(또는 Gaussian Splatting)로 전파되는 Gradient가 됩니다.
Diffusion Model의 Loss
수식으로 정리해보겠습니다. 먼저 Diffusion Model 수식으로 시작 해보겠습니다.

DDPM 이전글을 토대로 설명하자면, 입력 이미지에 특정 가우시안 노이즈가 추가되고, U-Net를 통해 생성한 가우시안 노이즈로 빼주면서 새로운 이미지를 생성하게 됩니다. 위 Loss는 U-Net parameter 업데이트를 위해 사용됩니다.
네트워크Φ 결과값과 입력이미지 x 간의 차이(diff)를 찾는 수식으로 정의되며, time t가 0~1 실수범위에서 uniform하게 얻어지고, 가우시안분포인 ϵ로 [ ]안의 값을 샘플링하였을 때의 기대(평균)값을 계산하는 수식으로 정의됩니다. w(t)는 time t에서의 가중값을 의미하고, ϵΦ는 U-net network로 reparameterization trick을 사용해서 확률분포를 입력이미지(x) + 표준편차(σ)*가우시안분포(ϵ) 수식으로 변형해서 network의 입력값으로 사용됩니다. 이 network의 결과값은 가우시안 분포(ϵ)를 따르도록 설계됩니다. 가우시안 분포를 따르지 않을 경우 Loss가 커지게 됩니다.
SDS(Score Distillation Sampling) Loss
이제 SDS Loss를 보겠습니다.

DreamFusion에서 x는 입력 이미지가 아니고 NeRF로 생성된 이미지이기 때문에, NeRF parameter θ를 가진 differentiable generator g으로 정의할 수 있습니다. Diffusion model loss와 비교했을 때, y가 추가된 것을 볼 수 있습니다. y는 Text를 임베딩한 값이 됩니다. Text to 3D가 아닌 Image to 3D로 만들 경우 y에 이미지를 넣으면 됩니다.
앞서 제가 'SDS Loss는 NeRF로 생성한 값과 임베딩값을 입력으로 U-Net을 통과해서 생성된 결과값이 2D diffusion prior학습시 사용된 이미지의 확률분포와 유사하지 않을 경우 Loss가 커지게 설계된다'라고 표현 하였는데, 이를 수식에서 보자면, 'text 임베딩 값'으로 zt (latent) vector를 만들고, zt가 U-Net을 통과해서 나온 결과 분포가 가우시안 분포를 따르면 Loss가 작아지도록 만들어져 있습니다. 이 값과 w(t)와의 곱이 gradient의 크기에 해당됩니다.
수식의 가장 오른쪽 미분 형태를 설명하자면, zt를 구성하고 있는 값은 NeRF Parameter θ로 만들어진 이미지 x이기 때문에 이미지x에 대해 θ로 미분하여, θ의 gradient를 계산하는 수식이 됩니다.
SDS Loss 수도코드
수도코드로 한번 더 설명해보겠습니다.
네트워크가 과정을 앞서 소개한 개념들과 SDS(Score Distillation Sampling) Loss를 함께 설명한 수도코드입니다.

1~3 : NeRF generator, optimizer, diffusion model을 초기화하고 로드합니다.
5 : diffusion model의 time step t가 uniform하게 정의됩니다.
6 : 시간 t에 따라 noise의 정도를 결정하는 alpha와 sigma가 정의됩니다.
7 : 이미지 크기만큼 가우시안 분포로 노이즈를 만듭니다.
8 : NeRF를 통해 이미지 x를 만듭니다.
9 : reparameterize trick을 통해 가우시안 확률분포를 계산 가능한 수식으로 만듭니다. z_t로 계산됩니다.
10 : z_t와 text embedding y, t를 입력으로 U-Net을 통과합니다.
11 : 위에서 언급한 아래 수식을 계산합니다. Diffusion Model은 업데이트 안하기 때문에 stopgradient가 사용됩니다.

12 : NeRF의 params와 optimizer의 state를 업데이트 합니다.
세부 유도 과정
아래는 수식 유도과정에 대해 다룹니다. 깊이 보실 분만 더 읽으시면 됩니다. Loss식에서 θ대해 gradient를 계산하면, 아래 수식이 됩니다.

네트워크 ϵΦ의 parameter가 바뀌었는데, y는 text를 embedding한 값을 의미하고, zt는 NeRF결과값(x) + 표준편차(σ)*가우시안분포(ϵ)식이라 생각되어집니다. Noise Residual은 x^2을 미분해서 2*x가 되었고, U-Net Jacobian은 ϵΦ가 zt을 입력으로 갖기 때문에 나온 수식이고, Generator Jacobian은 x가 θ을 입력으로 갖기 때문에 나온 수식입니다. DreamFusion에서는 실험적으로 U-Net Jacobian 부분이 상당한 연산량을 가졌고, 학습에 작은 noise만 줄 뿐, 큰 영향을 주지 않는 것을 확인했습니다. 그래서 U-Net Jacobian term을 생략했더니 효과적으로 gradient를 계산 할 수 있었다고 합니다.

위 수식으로 어떻게 training가능한지에 대해서 Appendix A.4에서 소개하고 있습니다. 위 수식과 아래 수식은 같습니다.
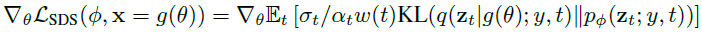
수식이 복잡한데, Text-to-3D 후속 논문들에서 계속 나오는 Loss라서 좀 더 설명해보겠습니다. 일단 바로 위 수식은, diffusion model으로 학습된 score function을 사용한 weighted density distillation loss(2018)로 부터 영감을 받아 만든 gradient라고 합니다.

'NeRF로 랜더링한 이미지 x가 주어질 때, 고정된 noise로 zt를 만드는 확률분포 q'와 '텍스트로 임베딩된 y가 주어질 때, U-Net parameter Φ에 따라 다른 zt를 만드는 확률분포 pΦ' 간의 KL-Divergence를 최소화 하기 위해 위의 식을 계산합니다. 가우시안 분포 ϵ로 샘플링한 기대값 공식으로 바꾸게 되면 우측항이 되고, x 생성에 사용되는 NeRF Parameter θ에 대한 gradient를 계산하면 (A)와 (B)로 구성된 두번째 식으로 만들어집니다. (A) term에서 q는 고정된 noise가 사용되기 때문에 미분값은 사실상 0입니다.

Sticking-the-Landing(2017) 연구에 따르면 (A)의 score function(=log probability의 gradient)를 제거할 경우 variance가 줄어들었다고 합니다. 그래서 parameter score만 제외하고 path derivative부분은 사용합니다.
(B)식까지 살펴보면,


위와 같은 수식이 되고, 이를 조합할 경우 아래 수식이 됩니다.
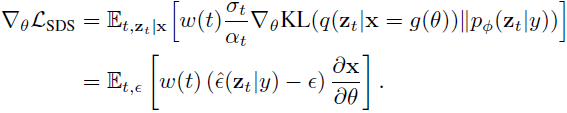
실제적으로, 가우시안분포 ϵ 이 부분은 lower-variance gradient를 가지면서 빠른 속도로 수렴하게 만들고 더 좋은 퀄리티를 보였다고 합니다.
그외 SDS Loss가 언급된 논문에 대한 세부내용은 [논문리뷰] DreamFusion (ICLR 2023) 에 있습니다.
'Terminology' 카테고리의 다른 글
| [개념 정리] Barycentric Coordinates : 질량 중심 좌표계 (1) | 2023.11.26 |
|---|---|
| [개념 정리] TV Loss (Total Variation Loss) (2) | 2023.10.24 |
| [개념 정리] 3D Gaussian의 Rasterizer (3) | 2023.09.27 |
| [개념 정리] Graphics에서 Spherical Harmonics (4) | 2023.09.20 |
| [개념 정리] Marching Cube : 3D Point to Mesh생성 알고리즘 (1) | 2023.08.21 |




댓글