TV Loss 소스코드
코드로 보면 개념 파악은 간단합니다. (코드 출처 : link )
def tv_loss(img):
xv = img[1:,:] - img[:-1,:]
yv = img[:,1:] - img[:,:-1]
loss = sum(abs(xv)) + sum(abs(yv))
return loss단일 이미지의 image의 수직축 수평축 각각에 대해 옆 픽셀간의 variation(변화량)을 구하고 summation합니다.
Loss이지만 predict이미지와 GT이미지 간의 비교형태가 아닙니다.
때문에 TV Regularization (Total Variation Regularization) 이라 부르기도 합니다.
이미지 생성 모델에서는 spatial smoothness를 만드는데 사용한다고 합니다. (link)
TensorFlow API에서 Total Variation Loss
TensorFlow API에서는 다음과 같이 소개 되어 있습니다. (link)
Total Variation은 입력 이미지에서 이웃 픽셀간의 차이의 절대값의 합입니다. 이미지의 noise를 줄이기 위해 Optimization 단계에서 Loss함수로 사용 될 수 있습니다. 이미지 batch를 갖고 있다면, 아래 코드를 통해 scalar loss값을 계산할 수 있습니다.
loss = tf.reduce_sum(tf.image.total_variation(images))Loss에 대한 별다른 설명이 없고, Wikipidea에 "Total Variation Denosing" 설명이 많길레 추가적으로 정리해봤습니다. (link)
Total Variation Denosing

이미지 잡음 제거 기법중에 하나입니다. Noise 영상에서 Signal의 total variation을 줄이면, 필요한 경계선은 유지하면서 필요없는 noise들을 제거하게 됩니다. 1D Singal Denosing부터 보겠습니다. (위 이미지 출처 : link )
1D Signal

Noise한 입력 신호xn(=회색선)에 디지털 신호yn(=검정선)를 근사(=E)시키고, yn과 yn+1에 대한 차이를 작게(=V)하는 것을 목표로 합니다. xn과 yn의 관계식은 다음과 같이 표현됩니다.
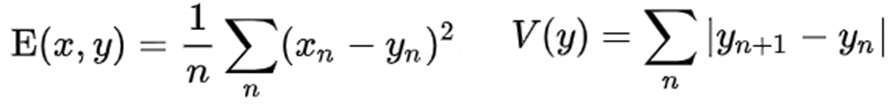
그리고 아래 수식을 최소화합니다.

이는 convex function(볼록 함수)이기 때문에, y를 미분하면서 convex optimization을 통해 최적의 y를 찾게 됩니다.
Regularization Parameter
λ(람다)는 regularization parameter이며 중요한 역할을 합니다.
λ가 0이면, 디지털 신호 yn과 입력 신호 xn가 동일해지고 smoothing효과가 사라지게 됩니다.
λ가 무한대이면, 입력 신호 xn과 무관하게 디지털 신호간(yn과 yn+1)의 변화량이 적어지게 됩니다.
TV Loss에선 입력신호 xn이 없으므로, λ가 무한대인 형태라고 보면 됩니다.
2D Signal Image
E + λ*V를 최소화하는 y를 찾는 것은 똑같습니다. 여기서는 y를 pixel색상으로 보면 되고, i는 x좌표, j는 y좌표에 해당합니다. 함수 E는 1D signal에서 root가 씌워진 L2 Norm 형태로 만들어집니다(<-중요하지 않은 내용). V를 보면 인접한 pixel들에 대해 x축으로 variation을 계산하고, y축으로 variation을 계산하는 형태입니다.

위 수식은 1992년에 나온 수식이며 istoropic(=모든 방향으로 동일한 특성을 가짐)한 형태가되어 미분이 불가능합니다. 때문에 이를 변형하였고, 아래 수식과 같이 anisotropic(=방향마다 다른 특성을 가짐)한 형태로 바꾸면, 쉽게 optimization 가능하다고 합니다.
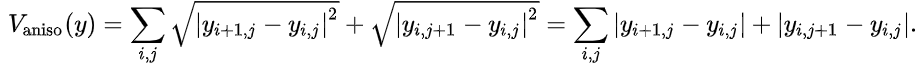
Total Variation Loss에 대한 기원은 찾지 못하였지만, Total Variation Denoising으로 부터 나오지 않았을까 추측해봅니다.
'Terminology' 카테고리의 다른 글
| [개념 정리] Anisotropic과 Isotropic (1) | 2023.12.13 |
|---|---|
| [개념 정리] Barycentric Coordinates : 질량 중심 좌표계 (1) | 2023.11.26 |
| [개념 정리] SDS(Score Distillation Sampling) Loss : Text-to-3D Loss (0) | 2023.10.12 |
| [개념 정리] 3D Gaussian의 Rasterizer (3) | 2023.09.27 |
| [개념 정리] Graphics에서 Spherical Harmonics (4) | 2023.09.20 |




댓글