BARF : Bundle-Adjusting Neural Radiance Fields, Chen-Hsuan Lin (ICCV2021)
NeRF에서는 Camera Pose가 이미지와 쌍으로 항상 주어져야 하지만 BARF에서는 Camera Pose가 주어지지 않을 경우에도 3D Scene Representation을 할 수 있게 하였습니다.
여러장의 Image에 대해, 대한 불확실한 카메라 pose값이 주어지거나 카메라 pose가 전혀 주어지지 않을 때, Camera Pose를 조정하고(Registration), 3D Scene Representation을 하는 방법에 대해 소개합니다. 이전 연구 NeRF– 에서는 2-stage pipeline 으로, unknown 카메라 pose를 추정하였지만, BARF에서는 수학적으로 Camera Pose와 3D Representation을 동시에 최적화 하는 방법을 소개합니다. 논문이 어려워서 사실상 완전히 이해 못했습니다. 해당 논문 리뷰는 참고용으로 보시길 바랍니다.
제안하는 문제는 다음과 같습니다.
BARF를 요약하자면 아래 수식으로 설명 될 수 있습니다.
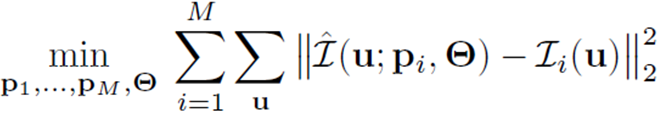
각 이미지 i에 대한 Camera Pose p와 MLP weight Θ가 주어졌을 때, Pixel 좌표 u에 대한 radiance 값을 출력하는 함수가 GT의 radiance 값 과의 오차를 줄이도록 Camera Pose p와 MLP weight Θ를 최적화하는 방법에 관해 설명하고 있습니다.
논문의 기여는 크게 3가지 입니다.
- 이미지에 대한 pose값과, NeRF reconstruction에 theoretical connection을 만들었습니다.
- Pose Estimation을 동시에 할 수 있게, Positional Encoding 을 개선한 coarse-to-fine registration 전략을 사용했습니다.
- Unknown pose로부터 video sequence의 view synthesis와 localization을 가능하게 하였습니다.
Imaging Function
BARF에서 소개한 Pixel location u에서 RGB color를 계산하는 수식 I(u)는 다음과 같습니다.

위 식은 original NeRF에서 언급된 Volume Rendering 기반한 pixel에 대한 Color 수식인 아래 수식과 유사한 형태의 수식입니다.

아래 r(t)와 위의 z*u는 3D Voxel 좌표를 의미합니다. 2개 식의 다른 점은 r(t)가 z와 U로 표현되었다는 것인데, original NerF에서 r(t)는 view direction 을 기반으로 하여 camera to world coordinate matrix를 사용해 ray위의 점을 샘플링 하였었다면, BARF에서는 pixel좌표(u) 에서 camera 를 기준으로 깊이(z) 에 있는 좌표를 샘플링을 합니다.
U는 2차원이고, 1을 3번째 차원에 넣어준 후, 깊이값 z를 모든 차원에 곱해줌으로써, 3D Voxel Point를 획득하게 됩니다.
BARF에서는 Origin NeRF와 동일하게 Discrete하게 샘플링을 하게 되며, pixel u에서의 RGB Color는 I(u)는 다음과 같은, g와 f에 대한 수식으로 정의됩니다.

g는 ray 위 에서 sampling 된 N개의 Point 들을 MLP로 통과 시킨 결과 y값들을 입력으로 가집니다.
f는 weight(Θ)를 가진 MLP이고, 3차원 좌표값(x)를 입력으로 하여 color(c)와 volume density(σ)를 출력합니다.
위의 식까지는 (3D Voxel Points 좌표 계산 부분을 제외 하고) Original NeRF를 다른 수식으로 표현했다고 생각하면 됩니다. 아래부터는 camera pose개념이 들어가는 수식으로 parameter가 추가됩니다.
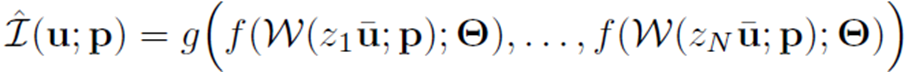
f는 weight (Θ)를 가진 MLP이고, W함수의 결과값을 입력으로 갖습니다. W는 warp functio이라고 하며, camera pose(p)변화에 따라, pixel u좌표에서 샘플링한 point(z*u)의 좌표를 선형 변환합니다.
I(u;p)는 Camera pose가 주어졌을 때, Pixel Coordinate에서 좌표z에 대한 RGB color를 계산하는 수식입니다.
Optimization
위의 Image Function을 기반으로 최적화 공식을 만듭니다.

M개의 이미지가 주어졌을 때, Neural Radiance Field 와 camera pose 둘 다를 동시에 optimization 하는 것을 목표로 합니다. Pixel 좌표계의 각각의 u 좌표에 대해, MLP로 획득한 Color값(좌항)과 이미지 상의 Color값(우항)의 차이를 최소화하도록, 각 이미지의 pose parameter 와 MLP f의 Weight를 같이 업데이트 합니다.
이 식을 계산하기 위해, Optical Flow에서 사용되는 Lucas-Kanade 알고리즘을 사용하게 됩니다. Optical Flow에 대해서는 https://gaussian37.github.io/vision-concept-optical_flow/ 에 잘 설명 되어 있습니다. Optical Flow는 시간 t 변경에 따라 각 픽셀 좌표들의 변화량 vector(=motion vector)를 구하였지만, BARF에서는 카메라 pose 변경에 따른 각 픽셀 좌표의 변화량 vector 를 구하는 수식으로 바뀌게 됩니다. Optical Flow의 Lucas-Kanade 알고리즘에 대해 설명하자면, 극소 영역(3x3픽셀)이 동일한 Motion 변화량을 가진다는 전제를 갖고, 시간 변화에 따라 각 픽셀 좌표 변화량 v를 계산하는 알고리즘입니다. 아래와 같이 식이 정의 됩니다.
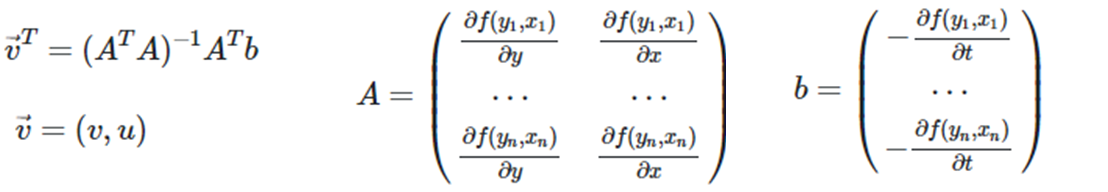
수식에 대해 설명하자면, 각 좌표에서의 변화량 vector v는 해당 좌표 주변의 픽셀에 대해, 픽셀 좌표의 색상 값을 출력하는 f함수를 각 dimension x, y으로 편미분한 행렬 A와 f함수를 시간으로 편미분한 행렬 b로 구성이 됩니다.
BARF에서 언급된 수식은 다음과 같습니다. 위와 비슷한 형태의 수식이며, Camera pose변화에 따라 픽셀 좌표 변화량을 계산하는 수식이 됩니다.
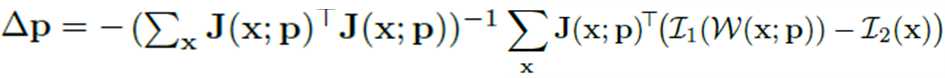
입력값 x는 x좌표,y좌표를 모두 포괄하며, 픽셀 좌표변화량 만큼을 Camera Pose의 변화량 △p 으로 설정합니다.
Backpropagation을 통해 효과적으로 camera pose △p 를 update하고, 일관되게 geometric 변위를 예측할 수 있도록 합니다.
J는 특정 pixel 좌표 x를 입력으로 색상 값 출력 함수 I에 대해 camera pose parameter p로 편미분하는 수식입니다. Jacobian개념이 들어가게 되는데, 극소 영역에서 비선형 변환을 선형 변환으로 근사시키는 Matrix를 Jacobian이라고 합니다. 아래와 같이 3개의 Jacobian으로 표현이 됩니다. (정확하지 않은 것 같아 삭제)

Jacobian 개념 참고 : https://angeloyeo.github.io/2020/07/24/Jacobian.html
Positional Encoding
다음으로 Positional Encoding에 관한 내용입니다.
NeRF의 Positional Encoding을 그대로 사용할 경우, 샘플링한 3D Point에 관한 gradient 값이 일관되지 않기 때문에 camera pose값을 Update하기 어렵습니다. (실제 논문에서는 더 자세히 설명 되어있습니다. 이해가 되지 않아 다 옮기지 못했습니다.)
BARF에서는 아래 수식으로 positional encoding 을 수정하였고, α값을 0에서부터 L까지 점점 증가시킴으로써, 초기에 smooth 한 signal 로 pose를 registration 하고, 뒤쪽에서는 high-fidelity signal을 볼 수 있도록 설계하였습니다. Coarse-to-fine registration 전략이라고 표현되고 있습니다.
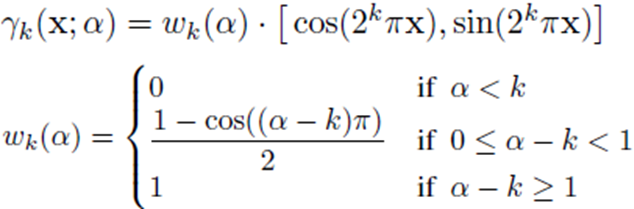
논문에서 r 함수에 대한 gradient를 아래와 같이 언급 해두었습니다. Original NeRF에서는 positional encoding의 결과값이 MLP의 입력값이기 때문에, gradient를 계산하지 않아도 됩니다. BARF에서는 J(u;p) 를 계산할 때 쓰이지 않을까 합니다.
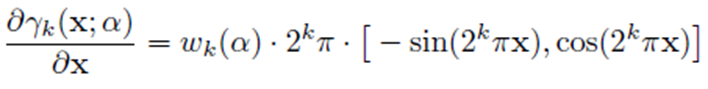
실제 논문에서는 Positional Encoding을 다룰 때, 소제목이 Bundle-Adjusting NeRF라고 표현되어 있습니다. 논문 제목이기도 합니다.
Experiments - Planar Image Alignment (2D)
위에서 3D 카메라 Pose에 대해서만 언급하였는데, 실제 논문에서는 2D pose에 대해 먼저 언급되어 있으며, 2D상에서 2D Pose도 추정하면서 랜더링을 할 수 있습니다. ImageNet에서 아래와 같은 5(=M)장의 랜덤 Patch가 주어질 때, pose parameter를 찾으면서 representation을 학습하는 Task를 잘 해결 하는지 실험하였습다.
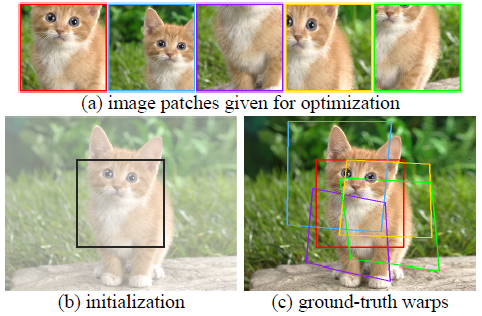
MLP는 256 unit을 가진 4개 hidden layer로 구성하였습니다. 학습시 총 5000 iteration을 진행하였고, 초기 2000 iteration은 Positional Encoding의 α값을 linear하게 증가시켰고, 나머지 3000 iteration은 α를 L(=8)로 두고 학습하였습니다.

NeRF의 Positional Encdoing을 사용할 경우, positional encoding이 전혀 없을 경우, BARF의 Positional Encoding을 적용하였을 경우의 결과입니다. 세부적인 PSNR 수치로는 다음과 같습니다.
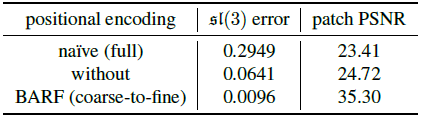
BARF의 Positional Encoding의 효과를 알 수 있습니다.
Experiments - NeRF(3D) : Synthetic Objects
100(=M)개의 이미지로 구성된 original NeRF의 object-centric scene 8개에 대해 실험하였습니다. camera pose는 extrinsic matrix 형태인 se(3) Lie algebra(https://edward0im.github.io/mathematics/2020/05/01/lie-theory/ 참고)로 되어있고, Intrinsic matrix는 주어집니다.

각 Scene에 대해서, 추가적인 noise를 줍니다. rotation에 대해 14.9도로 표준 편차를 주고, 이동 변환에 대해 0.26 크기로 표준 편차를 주었습니다.
Original NerF의 Architectural setting을 따르면서 지금부터 언급되는 부분만 다릅니다. NeRF의 구조는 다음과 같습니다.

Original NeRF는 layer마다 256 hidden unit이었지만 BARF에서는 128개로 사용합니다.
Original NeRF는 coarse Sampling, fine sampling으로 나누어져 있지만, BARF는 Sampling이 1단계로만 되어 있습니다. 이때 1개 Ray당 128개 point를 샘플링합니다. BARF는 image를 400x400 해상도로 바꾸고, 각 step마다 1024 pixel ray를 랜덤하게 샘플링합니다. NeRF에서는 Relu를 썼지만, BARF에서는 softplus를 사용했습니다. Adam optimizer를 썼고, 200K iteration 학습했습니다. network f에 대해서는 0.0005 learning rate로 decaying 0.0001, pose p에 대해서는 0.001 learning rate로 decaying 0.00001 로 셋팅했습니다. Positional Encoding의 α값에 대해 20K~100K까지 linear하게 증가 시켰고, 그 이후로는 α 를 L(=10)로 두어 all frequency bands를 사용 할 수 있도록 했습니다.
pose error와 view synthesis quality에 대해 평가하였습니다. pose에 대해서는 평균 rotation, translation error를 측정하였고, View Synthesis에 대해서는 PSNR, SSIM, LPIPS를 측정하였습니다. -> 평가 지표 Link

모든항목에 NeRF의 Positional Encoding 셋팅, Positional Encoding이 없을 경우, BARF의 Positional Encdoing에 대해서 측정하였습니다. ref NeRF라고 표시된 부분은 카메라 parameter가 주어졌을 경우 성능을 의미하고, 다른 부분은 위에서 설명한 대로 extrinsic parameter가 imperfect하게 임의로 조정하였을 경우의 성능을 나타냅니다. Image Quality적으로 볼 때, imperfect pose환경에서의 BARF가, perfect pose환경에서의 NeRF의 성능이 비슷한 것을 볼 수 있습니다. 그리고 전체적으로 보면 NeRF의 Positional Encdoing을 사용할 경우 성능이 좋지 않다는 것을 확인 해볼 수 있습니다. positional encoding이 없는 경우 BARF와 성능 차이가 크지 않게 약간 낮은 것을 볼 수 있습니다. pose registration 관점에서는 거의 정답과 근사하게 estimation한 것을 볼 수 있습니다. chair scene에 대한 결과입니다.

Experiments - NeRF(3D) : Real-World Scenes
손으로 직접 촬영한 8개의 정면 scene으로 구성된 LLFF 데이터셋에서 (SfM 으로 측정된)pose정보를 제외하여 성능을 측정하였습니다. Camera Extrinsic matrix는 모두 0으로 초기화되어 있고, Camera Intrinsic만 주어지게 됩니다.
학습시, 480x640으로 resize하고, 200K iteration하고, 각 step 마다 2048pixel를 샘플링합니다. f network는 0.001 learning rate, 0.0001 decay, pose p에 대해서는 0.003 learning rate, 0.00001 decay로 두었습니다. Positional Encoding은 위와 동일하게 α값에 대해 20K~100K까지 linear하게 증가 시켰고, 그 이후로는 α 를 L(=10)로 두었습니다.
실험결과는 다음과 같습니다.
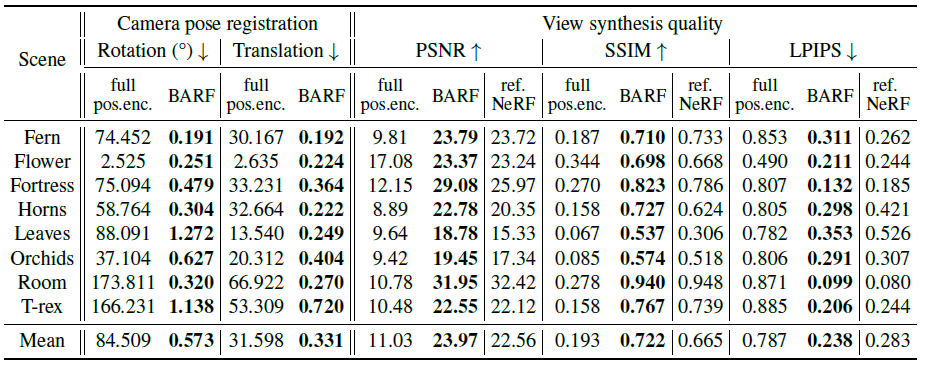
pose 추정에 대해서는 SfM 함수와 동일한지를 보게 되는데, 거의 동일한 수치를 보였습니다. Extrnsic parameter가 주어진 ref NeRF와 비교했을 때 더 좋은 성능을 보였습니다. 당연하게 NeRF의 Positional Encoding을 camera pose가 주어지지 않은 환경에서 사용할 경우 성능이 잘 나오지 않습니다.

Closing..
제목에 대해 생각해보면 논문 내 Introduction부분에서 Bundle Adjustment(BA)라고 언급해뒀는데, on both structure and cameras 라는 표현이 붙은 것을 보면, Camera Pose와 Representation이라는 bundle을 동시에 최적화 시킨다라는 의미로도 생각해 볼 수 있습니다. 이번 논문은 이해하는데 시간이 많이 쓰였고, Optical Flow에 관한 배경지식과 수학에 관한 지식이 필요해서 읽기가 어려웠네요. 코드가 공개되어 있으니 의지만 있다면 추후에 완전히 이해 할 수 있다고 믿습니다... Camera Pose가 없어도 되니, 많은 어플리케이션에서 쓰일 수 있을 것 같습니다.
'NeRF' 카테고리의 다른 글
| [논문 리뷰] Mip-NeRF (CVPR 2021) : Anti-Aliasing 연구 (2) | 2022.12.04 |
|---|---|
| [소스코드 분석] NeRF (ECCV 2020) (3) | 2022.11.26 |
| [논문 리뷰] Instant NGP(SIGGRAPH 2022) : 인코딩 방법 개선으로 속도 향상 (2) | 2022.11.10 |
| [논문 리뷰] MVSNeRF (ICCV2021) : 적은 입력 + 학습 속도 개선 논문 (0) | 2022.10.27 |
| [논문 리뷰] Plenoxels (CVPR 2022) : 학습 속도 개선 논문 (0) | 2022.10.20 |




댓글