Jensen's inequality는 볼록 함수의 기댓값에 관한 부등식입니다.

Random Variable X는 확률 변수에 해당됩니다. 관측값이기도 합니다.
Expectation E는 기대값으로써, 평균값입니다.
Function g는 Convex Function(볼록 함수)를 전제로 하며, 예시는 아래와 같습니다.


E(g(X))는 g함수값에 대한 평균값을 의미하며, g(E(X))는 X평균에 대한 g함수값입니다.
X는 확률 변수이기 때문에 g함수의 형태에 따라 E(g(X))와 g(E(X))가 다른 값을 가지게 되며, 볼록 함수일 때 Jensen's inequality라는 명칭으로 정의한 것 입니다.
증명은 Ox educ 유튜브(link)에 잘 소개되어 있으며, 2차원 g(x)를 미분한 1차원 함수 L(x)=a+bx를 기반으로 설명하고 있습니다. g(x)에 대한 기댓값은 L(x)의 기대값보다 크며, E[a+bx] = a+bE[x]가 성립하기 때문에, 위 수식을 만족한다라고 증명하고 있습니다. 이미지 내 오른쪽 아래 3줄 수식을 보시면 됩니다.

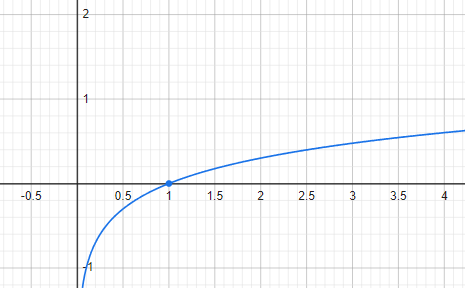
Concave Function(오목 함수)의 경우엔, 부등식이 반대로 됩니다.
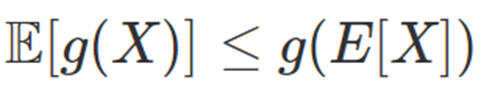
Concave Function(오목 함수)의 예시는 다음과 같습니다.

논문 읽을 때 한번씩 언급이 되서 따로 정리해보았습니다.
'Terminology' 카테고리의 다른 글
| [개념 정리] 수학 역삼각형 기호 의미 : 나블라(Nabla), 델(Del) (1) | 2024.01.02 |
|---|---|
| [기본 개념] CLIP (Contrastive Language-Image Pre-training) (2) | 2023.12.24 |
| [개념 정리] Anisotropic과 Isotropic (1) | 2023.12.13 |
| [개념 정리] Barycentric Coordinates : 질량 중심 좌표계 (1) | 2023.11.26 |
| [개념 정리] TV Loss (Total Variation Loss) (2) | 2023.10.24 |




댓글