F2-NeRF: Fast Neural Radiance Field Training with Free Camera Trajectories, Peng Wang, CVPR 2023
F2-NeRF는 NeRF모델의 속도를 개선하면서 퀄리티도 높이고 Unbounded Scene이 고려된 모델입니다. 아래는 저자 공식 페이지에 소개된 결과입니다.
NeRF의 학습 속도를 개선하기 위해 grid-based representation을 사용하는 연구들이 다수 발표되었습니다. 이러한 연구들은 학습 속도가 빠르지만 메모리 문제가 존재합니다. Plenoxel(이전글 link), DVGO은 voxel pruning 기법으로 이를 해결하였고, TensoRF는 tensor decomposition으로, Instant-NGP(이전글 link)는 hashing index로 해결하였습니다. 하지만 완전히 모든 scene에서 메모리 문제를 해결한 것이 아니라, object가 앞쪽에만 있는 forward-facing scene 또는 object가 중심에 있는 360도 object-centric unbounded scene과 같은 한정된 scene에 대해서만 다루고 있습니다.

F2-NeRF에서는 multi-object가 centric되고 카메라 trajectory가 기다란 scene을 free trajectory이라고 부르고 있으며, 이러한 free trajectory을 다룰 수 있도록 모델이 설계되었습니다. free trajectory scene의 경우, 불균등하게 영역 메모리가 할당되면서 성능이 하락하게 되고, scene안에 많은 영역들이 빈공간이 되면서 특정 영역들은 어떤 입력 이미지들에서도 안 보일 수 있다고 합니다. 기존 grid기반 연구들은 규칙적인 타일링 방식으로 전체 scene을 만들어서 이러한 emtpy space를 버리긴 하지만, 제한된 GPU 메모리 때문에 blur한 이미지가 만들어지게 된다고 합니다.
F2-NeRF에서는 free trajectory scene을 빠른 속도로 학습하기 위한 다양한 기법을 제안하고 있습니다.
Overview
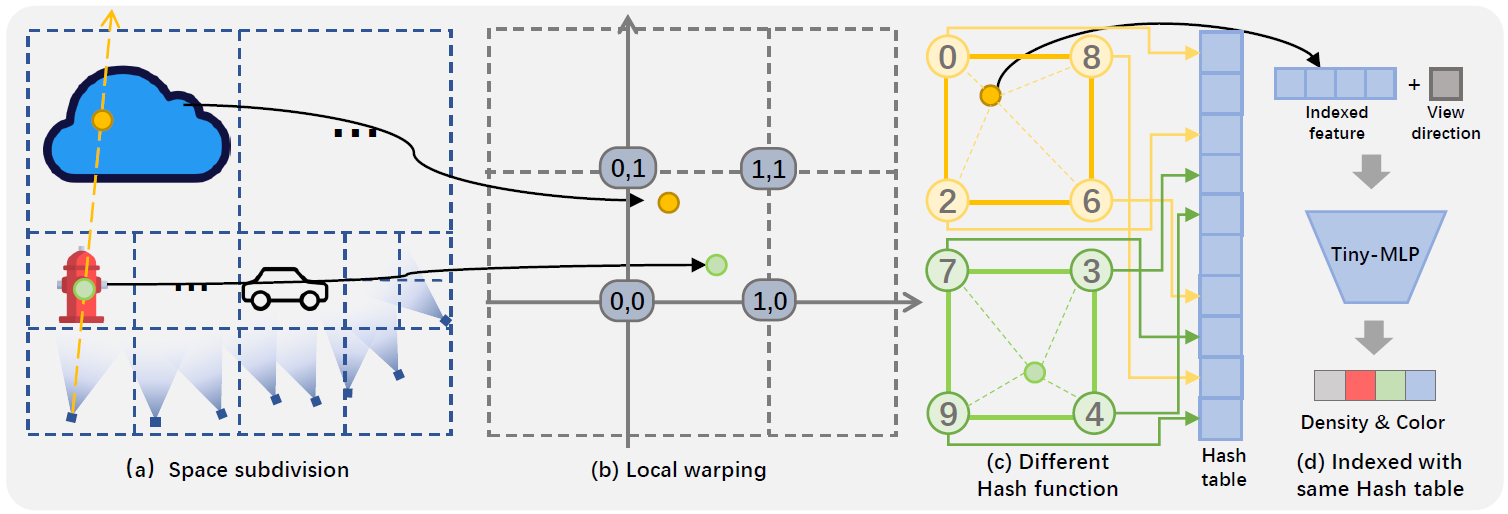
입력으로는 다른 NeRF연구와 마찬가지로, 카메라 pose와 해당 pose에서 촬영한 이미지들이 주어집니다.
크게 Preparation Stage과 Rendering Stage로 나뉩니다. (논문 내 소제목들과 #를 괄호안에 표시했습니다.)
- Preparation Stage는 카메라를 기준으로 전체 space을 sub-space로 나누고(3.3 space subdivision), 좌표를 임의의 space로 이동(3.2 perspective warping)합니다.
- Rendering Stage에서는 perspective에 따라 ray로부터 point를 샘플링(3.5 perspective sampling)하고, pixel을 rendering(3.4 scene representation)합니다.
본 글에서는 데이터 흐름 순서대로 설명하겠습니다.
3.3 Space Subdivision
space는 octree data 구조로 구성됩니다. 초기엔 카메라 3D 위치 값들을 모두 포함하는 bounding box를 만든 후, 그 box 보다 512배 큰 크기로 3D bounding box를 만듭니다. 이 초기 3D bouding box가 root node가 되고, side length s와 상수값 λ=3이 주어집니다. 그리고 node는 특정 조건에 따라 8개의 sub-node로 나뉘고 sub-node의 side length도 s/2로 바뀝니다. 그 조건은 다음과 같습니다.
카메라에서 ray를 그렸을 때, 그 ray위의 sampling된 point가 node공간에 포함된다면, 해당 node공간에 대한 visible camera에 해당됩니다. root node는 모든 camera가 포함되어 있을 것 입니다. node의 중심점과 각 카메라의 위치의 거리가 d라고 하였을 때, d<=λs를 만족할 경우, sub-node로 나뉘어지게 됩니다. 이 과정을 사전 정의한 nl개의 leaf node가 나올 때까지 반복합니다.
node마다 visible camera가 최소 1개부터 무수히 많은 수가 있을 수 있습니다. 논문에서는 연산량을 줄이기 위해, 특정 node의 visible camera가 5개 이상이라면, 랜덤하게 visible camera를 선택 한 후, 선택한 카메라와 가장 멀리 있는 카메라를 선택합니다. 이를 4번 반복하여, node마다 최대 4개의 visible camera를 배정합니다.
subdivsion된 node에 대해 Camera Rectification라는 기법이 추가 적용됩니다.

각 node마다 visible camera들에 대해, 특정 거리 r만큼의 위치에서 node의 중심을 바라보게 하면, 더 좋은 성능을 보였다고 합니다.
3.2 Perspective Warping
이전 NeRF연구들에서는 unbounded scene을 표현하기 위해, bounded scene으로 mapping하는 space-warping 방법들이 제시 되었습니다. 최초 NeRF논문에서는 forward-front scene을 위해 NDC(Normalized Device Coordinate) warping을 사용했었고, NeRF++, Mip-nerf 360 에서는 object-centric scene을 위해 inverse-sphere warping을 사용했었습니다. F2-NeRF에서는 서론에 소개했던 free-trajectory scene을 위해, perspective warping을 제안합니다.
논문에서는 기존 방법론에 대한 문제를 그림을 통해 먼저 소개하고 있습니다.
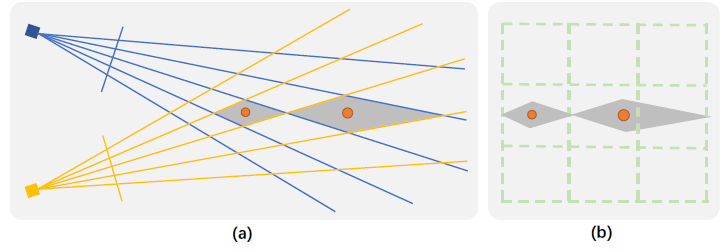
(a) 2개의 카메라로 주황색 2개점을 관측 할 때, 각 4개 ray에 대해 2차원으로 표현한 그림입니다.
(b) 같은 영상에 대해 Axis-aligned grid로 표현하였을 때 그림입니다.
(a)에서 각 카메라를 기준으로 1개의 pixel은 오른쪽 주황색 극소점에 대해, 오른쪽 회색 마름모 범위를 같은 color로 간주합니다. 반면, (b)에서 grid space로 주황점을 볼 경우에, 회색 마름모는 다른 구간 단위(초록색 점선)으로 나뉘어지게 됩니다. 이런 misalignment는 카메라로부터 거리가 멀어 질수록 더 크게 퀄리티에 영향을 주게 됩니다.
F2-NeRF에서는 어떻게 서로 다른 카메라들의 구간 단위를 alignment할지에 대해, 해결방법을 소개하고 있습니다.
1) 앞서 octree로 subdivision한 node마다 nc개의 visible 카메라에 대해, 한개의 3D point x를 각 카메라의 2D image plane으로 projection한 2d point list를 G(x)로 정의합니다. 3D point x는 original euclidean space에서 샘플링되었다고 표현하고 있습니다.

2) original euclidean space에서 warping space로 변환하는 함수를 F(x)라 하고, G(x)는 Matrix M을 통해 계산되어 집니다.

Matrix M는 PCA(Principle Component Analysis)기법을 사용해서, nc개의 2D point list들을 대표하는 주성분을 찾아 covariance matrix(공분산 행렬)로 정의되었습니다. PCA로 공분산 행렬을 만드는 방법에서 대해선, 공돌이 수학노트 PCA 참조 바랍니다. 논문에서는 아래 수식으로 sampling 3D points n개에 대한 2d points list인 K에 대해 공분산 행렬Q을 만듭니다. (K헷은 평균입니다.)

Q는 2nc x 2nc의 dimension으로 되어있습니다. nc개의 points list를 3d point로 만들기 위해, 상단 3개 행만 사용해서 Matrix M'을 만듭니다. (최종 M이 아닌 M'입니다.)

3) original euclidean space의 2D points가 warping space의 3D points로 변환 될 때 pixel의 unit length(최소 단위 크기)를 맞춰주기 위해 scale factor S가 추가 됩니다. Normalized 단계라고 부르고 있습니다.

(여기서부터 JW->I 수식 정의 부분까지 Skip하셔도 됩니다.) 논문에서는 각 행렬 변환을 Jacobian matrix로 소개하고 있으며, M'의 경우 original space O에서 image space I로 변환하는
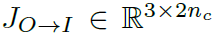
로 정의하고, 위에서는 M은 Image space I에서 warping space w로 변환하는 자코비안 행렬로 정의하고 있습니다. scale 값 계산시, warping space w에서 image space I로 변환하는 아래 자코비안 행렬로 정리하고 있으며, 각 column vector의 최대값이 1이 되도록 scale을 조절 했다고 합니다.
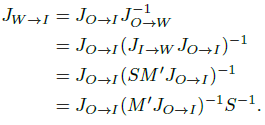
위 수식을 통해 node마다 warping function F(X)가 정의되며, 이를 통해 샘플링된 3D points가 node를 관측 할 수 있는 카메라 pose들에 align된 좌표 공간(perspective warping space)으로 변환 될 수 있으며, 이 좌표 공간에서 volume rendering수식을 적용하게 됩니다.
논문에서는 추가 내용으로 NDC warping과 inverse-sphere warping과의 관계를 설명하고 있으며, 이 두개를 perspective warping에서 커버하고 있다고 소개하고 있습니다.
본 단락은 서술형으로 작성이 되었는데, 요약하자면, 카메라들을 align하기 위해, euclidian 공간에서 normalized된 warping공간으로 변환시키는 함수가 설계되었다고 보면 되겠습니다.
3.5 perspective sampling
샘플링하는 방법에 관해 다룹니다. 위와 같이 주성분분석을 통해 warping함수를 만들게 되면, warping sapce에서 임의의 3d point 2개의 거리는 이미지 plane들로 projection했을 때 2d points 2개의 거리의 합과 동일하게 된다고 합니다. 때문에 warping space에서 uniform하게 샘플링하는 것은 실제 euclidian sapce에서는 non-unifrom하지만 안정적으로 수렴 할 수 있게 합니다. 이전 연구들에는 x = o + t*d (o:origin, t:카메라에서 떨어진거리, d:view direction) 공식으로 샘플링하였지만, F2-NeRF에서는, 첫번째 x에 대해 기준을 잡은 후에, 아래 수식으로 샘플링합니다.
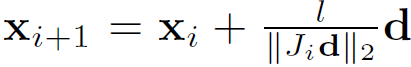
l은 sampling interval을 조절하는 상수값이고, J는 x에 대한 3x3자코비안 matrix입니다.
3.4 scene representation
서로 다른 leaf node의 점들을 0~1사이의 공간으로 맵핑하면서 iNGP 보다 충돌이 많이 발생하게 됩니다. F2-NeRF에서는 iNGP(이전글 link)의 Hash function을 개선하게 됩니다.
비교 설명을 위해 iNGP함수를 먼저 언급하겠습니다.

x는 입력 좌표와 근접한 grid의 3d vertex좌표, d는 dimension을 의미하고(3차원이기 때문에 3), π는 dimension마다 임의로 정해둔 실수값(𝜋1 := 1, 𝜋2 = 2 654 435 761, 𝜋3 = 805 459 861) , 십자가 표시는 비트별 XOR연산, T는 hash table의 size입니다. 위 수식을 통해 충돌을 최소화하여 Hash Value를 얻게 됩니다.
다음으로 F2-NeRF입니다.

x=v, L=T가 각각 동일한 의미로 맵핑이 됩니다. i가 추가되게 되는데, leaf node의 갯수만큼 존재합니다. 때문에 Hash function이 1개가 아니라 여러 개인 것을 알 수 있습니다. △i,k 는 offset값이며 𝜋와 동일하게 미리 정의된 상수값입니다.

때문에, 서로 다른 grid에서 획득한 2점이 warping된 space 같은 좌표값을 같더라도, 다른 hash table을 사용하기 때문에, 다른 값을 갖게 됩니다.
그외 Hash Table로 인코딩된 값이 MLP를 통과해서 color값을 얻는건 iNGP와 동일합니다.
Training Loss


color reconsturction loss와 두개의 regularization으로 구성되어 있습니다. Disparity Loss는 disparity(inverse depth)가 너무 크지 않게 하여 floating artifact를 줄여줍니다. Total Variance Loss는 2개 이웃 Octree nodes의 경계의 point들이 유사한 density와 color를 갖도록 해줍니다.
여기까지 알고리즘을 설명 했습니다. 위에서 언급한 4가지 소제목이 모두 F2-NeRF 핵심 키워드임을 알 수 있습니다.
space subdivision, perspective warping, perspective sampling, scene represnetation(Hash Function)
Experiments
데이터셋은 3가지로 사용되었는데, F2-NeRF에서 처음 제시한 좁고 긴 카메라 trajectories데이터셋인 Free dataset, forward-facing scene인 LLFF dataset, unbounded 360도 inward-facing scene인 NeRF-360-V2 dataset으로 실험하였습니다. 8개마다 1개를 testset으로 두고 나머지는 trainset으로 둡니다. 평가지표인 PSNR, SSIM, LPIS는 이전글 Link 참조 바랍니다.

Grid 계열 논문들과 비교하였을 때, 빠른 속도에 속하고, PSNR도 가장 좋습니다. 학습시 2080Ti GPU 1개를 사용했다고 합니다.

다른 데이터셋으로 평가했을 때도 비슷한 추이를 보이고 있습니다.

위표는 Basic한 모델(A)를 기준으로 inverse warping을 추가(B)하였을 경우, 성능 향상이 있었고, exponential sampling을 하였을 때 (C) 더 개선되었고, Perspecitve Warping (D)를 적용하였을 경우, Perspective Sampling을 하였을 경우의 상승 정도를 표현하였습니다.

mip-NeRF-360 결과는 30분동안 학습하였을 때의 결과이고, mip-NeRF360을 충분히 학습(1시간 이상)하면 F2보다 더 좋은 성능을 보였다고 합니다.
Closing..
넓은 Scene을 담으면서, High Quality로 랜더링하고, 메모리도 적게 사용하고, 학습 속도도 빠릅니다. 골고루 다 갖춘 모델이네요. grid 기반 연구가 계속적으로 발달하고 있습니다. 2022년 중반에 iNGP가 비약적으로 학습 속도를 개선시켰고, 이제 이를 기반으로 퀄리티를 개선하는 연구들이 나오고 있네요. 다음엔 어떤 turning point 연구가 나올지 기대됩니다.
'NeRF' 카테고리의 다른 글
| [논문 리뷰] Zip-NeRF (ICCV 2023) : Anti-Aliasing, 속도 개선 (1) | 2023.08.02 |
|---|---|
| [논문 리뷰] TensoRF (ECCV 2022) : 메모리/속도 개선 (1) | 2023.07.30 |
| [논문 리뷰] DreamFusion (ICLR 2023) : Text to 3D 연구 (6) | 2023.06.06 |
| [논문 리뷰] NoPe-NeRF (CVPR 2023) : Camera Pose Estimation & NeRF (3) | 2023.04.29 |
| [논문 리뷰] Mip-NeRF 360 (CVPR 2022) : Anti-Aliasing 연구2 (2) | 2023.04.22 |




댓글