NeRF와 SDF를 사용한 3D Reconstruction에 대한 연구입니다.
아래 그림을 먼저 보겠습니다. 진한 선이 surface에 대한 GT이고, 점선이 Prediction값입니다. 왼쪽은 Neural Surface Reconstruction 최신 연구인 IDR(2020년)을 사용할 경우이고, 오른쪽은 Neural Volume Rendering인 NeRF를 사용 했을 경우를 나타냅니다..
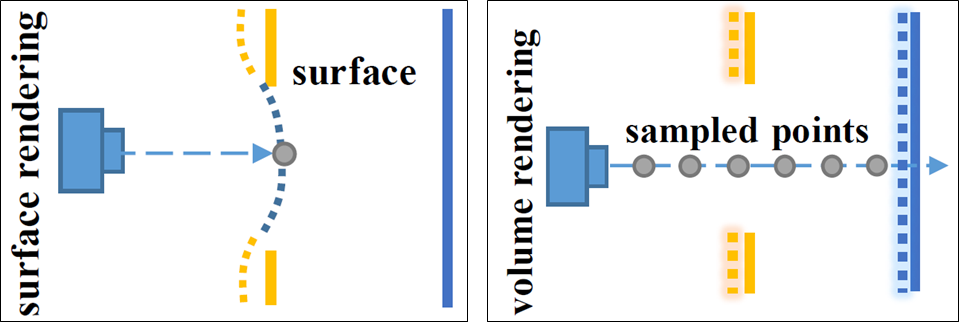
IDR에서는 급격한 depth변화가 있는 복잡한 구조 내 surface위의 single 3D point들에 대해 back propagation하기 때문에 local minimum 문제가 발생했습니다. 논문 저자는 NeRF의 경우 ray위의 sampling된 모든 points들이 back propagation 가능기 때문에 급격한 depth변화에도 강인 할 수 있다고 생각했습니다.
하지만 최초 NeRF는 surface reconstruction이 아닌 novel view synthesis에 초점이 맞춰져 있기 때문에 high-quality surface를 만들지 못했습니다. NeuS에서는 NeRF와 SDF representation을 사용해서 High Quality로 3D Reconstruction하는 방법에 대해서 다룹니다.

사전 지식
SDF(Signed Distance Fields) representation
Geometry관점에서 주어진 object의 내부는 +, 외부는 - , Surface에 근점 할 수록 0이되는 데이터 포맷입니다. 가장 가까운 surface까지의 거리를 표시합니다.( 출처 : link ) 비슷한 시기의 UNISURF라는 연구는 occupancy representation(내부는0, 외부는 1, 출처: link)을 사용했다고 합니다.

Logistic Density Distribution
NeuS에서 사용되는 핵심 함수입니다. Wikipedia에서 표현된 수식은 다음과 같습니다. unimodal형태의 종모양 입니다.

logistic density distribution(하단 좌측)을 적분하면 sigmoid 함수(하단 우측)가 됩니다.(출처 : link)

논문에서 사용되는 logistic density distribution는 아래 수식입니다. 위 wikipedia수식과 다른 점을 보면, 아래 수식은 μ(평균)이 0이고, s(표준편차)는 역수입니다.
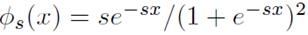
Overview
이번 논문은 수학입니다... 수식적으로 이해하려면 어렵기 때문에, NeRF연구와 차이점으로 설명드리겠습니다. NeRF에 대한 설명은 NeRF 이전글을 참고 바랍니다. 이전 글에서는 아래 수식을 생략했었습니다.
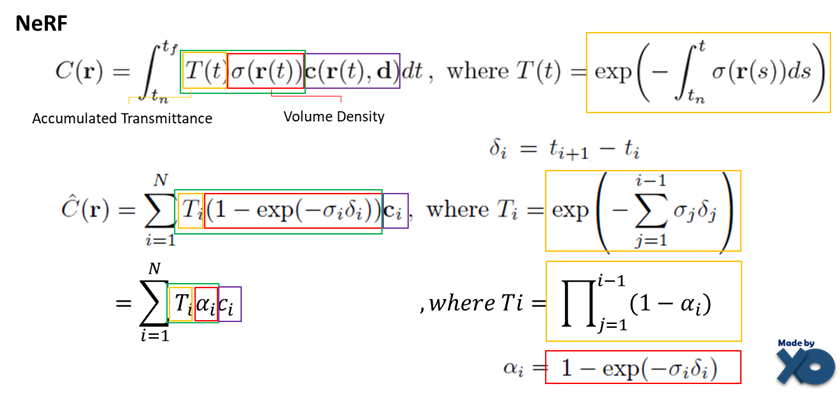
부연 설명하자면, Continuous한 공간을 표현하는 Integral식(C)을 Discrete한 공간으로 표현하기 위해 Sigma식(C헷)으로 변환되었습니다. Accumulated Transmittance * Volume Density * radiance 를 유지한 상태에서, Integral이 sigma형태만 바뀌는 것을 확인 할 수 있습니다.
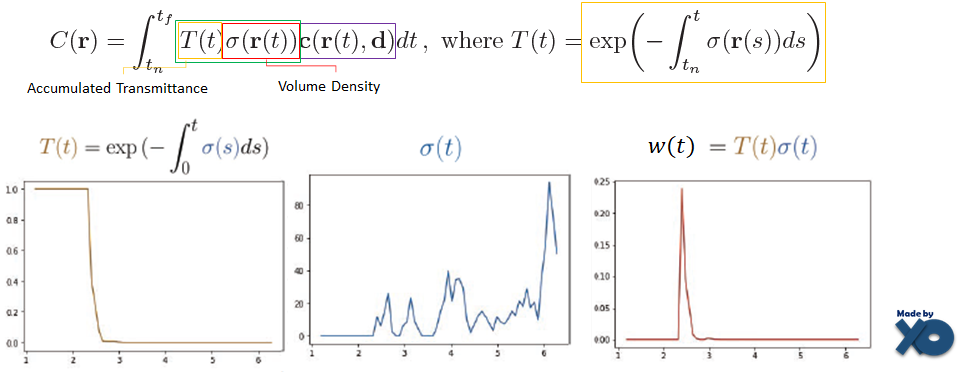
NeRF수식에서 Accumulated Transmittance인 T(t) 와 Volume Density인 σ(t)를 곱하면 Surface 영역을 검출 할 수 있었습니다. w(t) 그래프를 보시길 바랍니다. (아래 그래프는 후행 연구인 DS-NeRF에서 갖고온 이미지이며, x축은 카메라로 멀어지는 t좌표값, y축은 크기를 의미합니다.)
이 w(t)값을 SDF 값으로 사용하려고 하였지만 문제가 있었습니다. 아래 왼쪽 그래프를 보면, f(t)는 SDF함수이고, σ(t)는 Volume Density값 입니다. surface에 도달하기 전에 w(t)가 최대값을 가지는 것을 볼 수 있습니다.
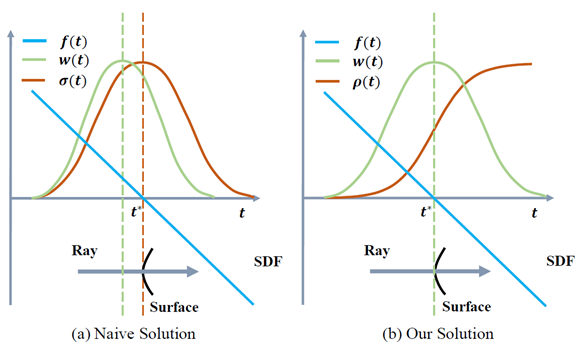
이를 해결하기 위해서, Volume Density인 σ(t)를 Opacity Density인 p(t)로 바꾸게 됩니다. 그럴 경우 w(t)가 SDF값과 일치하는 것을 볼 수 있습니다. σ(t)를 SDF 값으로 쓰면 되지 않나 생각되실 텐데, σ(t)만 있는 위쪽 그래프를 보시면 균일한 값을 가지지 않는 것을 볼 수 있습니다. 그리고 w(t)는 2가지를 만족해야 한다고 적혀 있습니다.
- Unbiased : 논문에서는 위왼쪽 그래프의 경우 bias가 발생했다고 표현하고 있습니다. surface에서 w(t)가 최대값을 가져야 됩니다. weight w(t)값이 pixel color를 결정하는데 가장 많이 contiribution 될 수 있도록 보장해야 합니다.
- Occlusion-aware : ray위의 다른 2개 t가 같은 SDF값을 가질 경우, view point 가까이에 있는 t가 더 많은 contribution되어야 합니다. ray가 multiple surface를 지날 때, camera 가까이에 있는 surface의 color가 사용 되어져야 합니다.
이를 만족하는 w(t)를 수식적으로 어떻게 설계하였는지 보겠습니다.

w(t)가 NeRF에선 T(t)*σ(t)였다면, NeuS에선 T(t)*α(t) 입니다. 두개 알고리즘을 비교하기 위해 색상으로 구분 가능하도록 표시해뒀습니다. 전체적으로 비슷한 형태로 가면서, 빨간색 박스 부분인 Discrete Volume Density에서 Discrete Opacity Density으로 바뀐 것을 볼 수 있습니다. Φ(x)는 앞서 설명드렸던 Sigmoid 함수를 미분한 함수인 logistic density distribution에 해당합니다.
위 수식을 사용하면 high quality의 SDF를 구현 할 수 있습니다. 논문 내용의 대부분은 저 수식이 어떻게 도출되었는지 과정을 설명하는데 써져있습니다.
수식 도출 과정
수식을 도출하는 과정을 설명해보겠습니다. 읽다가 중간에 "수식 도출 과정" 파트만 스킵하셔도 됩니다.
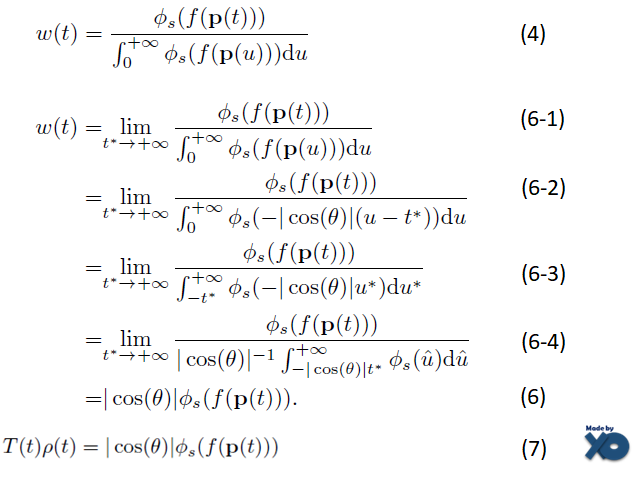
W(t)를 종모양으로 만들기 위해 , Logistic Density Distribution 함수 Φ 로 표현합니다.
(4)는 ray위의 모든 점에 대한 값을 분모로 가짐으로써, 함수 Φ 를 normalization한다는 의미를 가지는 수식입니다.
(6-1)에서부터는 (4)에 의해 surface t*가 카메라로부터 무한히 멀어 경우를 가정하여 수식을 전개 합니다.
(6-2)는 아래 (5-1)에 의해 계산되어집니다.

(5-1)은 SDF의 특성상 ray위에 있는 surface위의 t*와 샘플링된 t간의 거리를 구하는 것이 아니라, 샘플링된 t의 Normal Vector값을 사용해야 하기 때문에 만들어진 수식입니다. 이해를 위해 그림을 그려봤습니다.
(6-3), (6-4)는 Integral의 시작 범위를 변경함으로써, 단순화시킵니다.
(6)은 (6-4)의 Integral 수식부분이 1이 되면서 사라지면서 정리됩니다.
(7)은 (5)와 (6)에 의해 정리 됩니다.
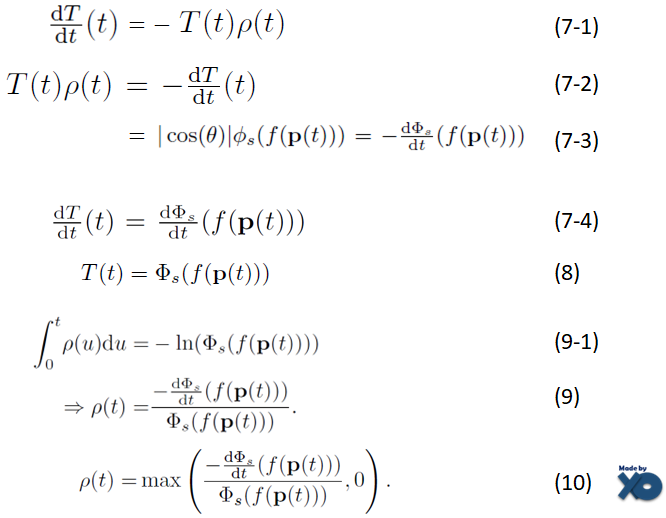
(7-1)은 exp(x)의 미분 특성에 의해, (5)를 참고하여 T(t)를 미분하면 계산됩니다.
(7-2)는 (7-1)에서 양변에 -1을 곱한 수식입니다.
(7-3) 좌항의 Φ은 Logistic density distribution, (7-3) 우항의 Φ는 sigmoid function 입니다.
Logistic density distribution을 미분하면, Sigmoid function이 됩니다.
(cos(Θ)는 (7-3)의 우항으로 가면서 생략된 것 같습니다. 이 부분은 정확히 모르겠습니다.)
(7-4)는 (7-2)와 (7-3)을 다시 정리한 수식이고
(8)은 (7-4) 양쪽 항을 적분한 수식입니다.
(9-1)은 (5)를 참고하여 (8)의 양쪽 항에 logarithm( = ln) 을 적용해줬습니다.
(9)는 (9-1)을 t로 미분한 수식입니다.
Opaque density 값이 음수가 되면 안되기 때문에, 최소값이 0이 되는 수식으로 (10) 식으로 바꿔줍니다.
수식 (10)은 continuous한 값인 Opaque Density에 대한 것입니다.
수식 (12~13)은 discrete한 값인 Opacity Density에 대한 것입니다.

(12)는 (9-1)에 의해 (20-1)이 되고 이를 전개하면 (20)이 됩니다.
Discrete Opacity Density가 음수가 되면 안되기 때문에, 최소값이 0이 되도록 (13)식으로 바꿔줍니다.
(13)이 최종적으로 사용되는 값입니다.
Training
학습방법도 NeRF와 비교해서 설명하겠습니다.
NeRF는 fine sampling과 coarse sampling을 구분해서 Image Plane에서 보여지는 Color값을 계산하고, GT와의 차이를 L2 Loss를 사용했습니다.

NeuS는 Color Loss, SDF 연구에서 많이 쓰이는 Regularization Loss, 물체의 pixel 영역의 GT와 비교하는 Mask Loss를 사용합니다. Mask Loss는 Option parameter로써, 없어도 동작합니다.

Color Loss는 NeRF와 다르게 L1 loss를 사용했습니다. 위에서 언급한 w(t)를 사용할 경우, outlier에 강인하고 stable했기 때문이라고 합니다.

SDF 분야에서 많이 쓰이는 Regularization Loss인 Eikonal term입니다.

Mask Loss는 Binary cross entropy loss인 BCE를 사용하였습니다.

NeuS는 NeRF와 Sampling기법이 다릅니다. NeRF에서는 uniform하게 split하여 분리된 구간 내 랜덤 샘플링하는 Stratified Sampling(=Coarse Sampling) 한 후에, w(t) 크기에 따라 t의 중요도로 샘플링하는 Inverse transform sampling(=Fine Sampling)을 했었습니다. Coarse Sampling한 점으로 학습시키는 네트워크를 Coarse Network, Fine Sampling한 점으로 학습시키는 네트워크를 Fine Network로 지칭했었습니다.
NeuS에서는 Coarse Network와 Fine Network를 동시에 학습합니다. coarse sampling은 ray위의 점들에 대해 아래 수식에서 표준편차 s를 고정시킨 상태로 sampling합니다. fine sampling은 학습되는 표준편차 s로 샘플링을 합니다. 표준편차 s는 학습되는 parameter로써, 위에 설계한 NeuS Loss를 사용 할 경우 수렴하면서 1/s가 0에 가까워지게 됩니다.
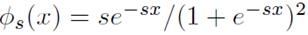
Experiments
Dataset
DTU에서 15개 Scene을 사용하고, BlendedMVS dataset에서 7개 Scene, 추가적으로 2개 Scene을 직접 촬영해서 사용했습니다.
DTU는 각 Scene마다 49개 or 64개 이미지로 구성되어 있으며, 1600x1200해상도를 가집니다.
BlendedMVS는 각 Scene마다 31-143개 이미지로 구성되어 있고, 768x576해상도를 가집니다.
논문에서 촬영한 2개 Scene은 32개 이미지로 구성되어 있습니다.
Speed
RTX2080Ti에서 mark loss를 사용할 경우 14시간, mask loss를 사용 안 할 경우 16시간이 Training 시간으로 소요됬습니다. 한개의 batch마다 512개 ray를 사용했다고 합니다.
Quality
DTU 데이터셋으로 비교한 결과입니다. mask를 사용할 경우 IDR과 NeRF와 비교하였고, mask를 사용하지 않을 경우 COLMAP, NeRF, UNISURF와 비교하였습니다. Chamfer Distance (설명 : link)로 GT와 Prediction간의 거리를 측정하여 평가하였습니다. mask를 무조건 사용해야하는 IDR이 3개의 Scene에서 우수한 결과를 보이지만 NeuS의 성능이 더 좋습니다.
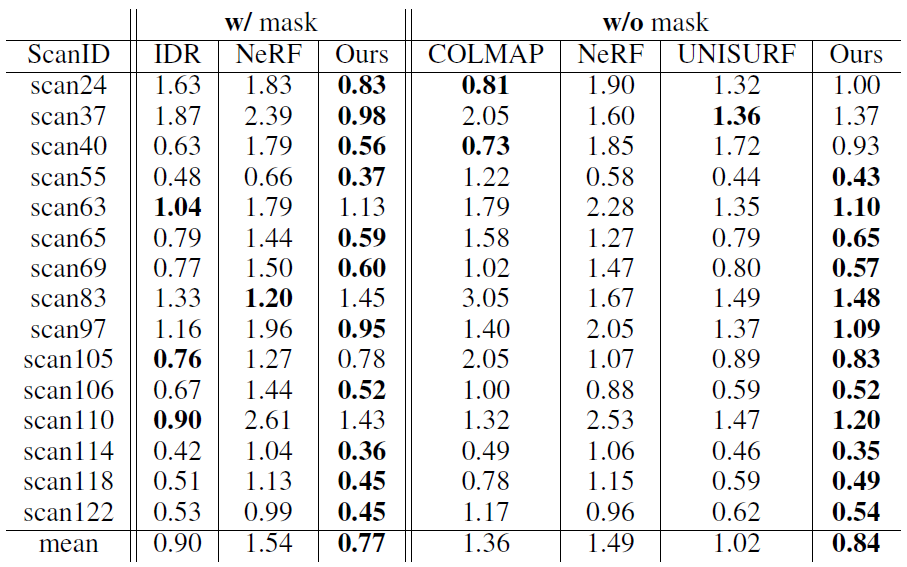
아래 그림은 Mask Loss를 사용한 결과입니다. IDR은 Scan37에서 Thine한 물체에 대해서 퀄리티가 좋지 않고, Stone Scene에서 급격한 depth 변화에 퀄리티가 좋지 않습니다. NeRF의 경우 전체적으로 Nosiy합니다. volume density field가 3D geometry에 대해 충분한 constraint를 갖지 못해서라고 합니다.

아래 그림은 Mask를 사용하지 않은 결과입니다. NeuS는 다른 연구들보다 fiedlity가 좋습니다. 급격한 depth변화에도 강인한 것을 볼 수 있습니다.

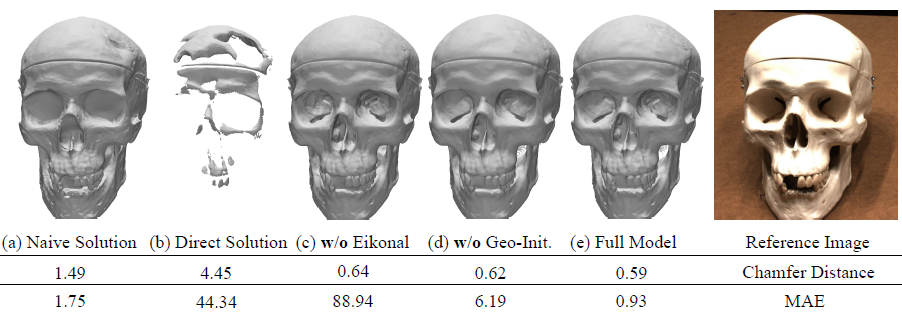
아래 그림은 설계에서 사용된 기법들이 얼마나 성능에 영향을 주었는지를 비교하는 Ablation Study입니다. MAE는 Mean Absolute Error입니다.
아래는 thin한 물체에 대해 32개 입력이미지로 학습한 결과입니다. 평면이 있는데 카메라 calibration(=camera paramter 획득 작업)을 위해 넣었다고 합니다. 아래 그림을 보면 thin 구조와 급격한 depth 변화를 가진 edge에서도 잘 되는 것을 볼 수 있습니다.

Limitation으로 Texture가 없는 경우에 성능저하가 발생하고 training시간이 오래걸린다고 합니다.
Closing..
NeRF를 리뷰하면서 SDF를 몇번 접해보니 이제 용어가 친숙해지네요. 이전에 논문 리뷰한 InstantNeRF 에서도 소개 되었었습니다. 빠른 속도로 SDF를 구성 하는 연구는 InstantNeRF 에서 볼 수 있습니다. SDF를 추정하는 연구가 Depth추정하는 DS-NeRF 연구와 비슷한 것이 아닌가 싶은데, 비슷해 보이면서도 surface가 중심이 되느냐, camera가 중심이 되느냐에 따라 다르네요. NeRF 분야에서 3D Reconstruction 도 하나의 큰 연구 주제가 될 것 같습니다.
'NeRF' 카테고리의 다른 글
| [논문 리뷰] Mip-NeRF 360 (CVPR 2022) : Anti-Aliasing 연구2 (2) | 2023.04.22 |
|---|---|
| [논문 리뷰] FreeNeRF (CVPR 2023) : 적은 입력 + 퀄리티 개선 연구 (0) | 2023.04.14 |
| [API 리뷰] NeRF Studio : NeRF 통합 Framework (10) | 2023.02.27 |
| [논문 리뷰] NICER-SLAM (3DV 2024) : NeRF접목 dense RGB SLAM (2) | 2023.02.15 |
| [논문 리뷰] NeRF-Art (arXiv 2022) : Text 입력 Style 변형 연구 (0) | 2023.02.11 |




댓글