1부에서는 SfM 기본 개념과 역사를 다뤘습니다.
[개념 정리] SfM(Structure from Motion) of COLMAP - 1부
COLMAP은 SfM(Structure from Motion)과 MVS(Multi-View Stereo)를 범용적으로 사용 할 수 있게 만든 라이브러리입니다.SfM은 이미지들을 입력으로 받아 Camera Parameter와 Point Cloud를 생성하고MVS는 'SfM 결과값'을 입
xoft.tistory.com
2부에서는 COLMAP SfM논문에서 제안하는 3가지 전략 Scene Graph Augmentation, Next Best View Selection, Robust and Efficient Triangulation에 대해 다뤘습니다.
[개념 정리] SfM(Structure from Motion) of COLMAP - 2부
SfM of COLMAP 1부에선 SfM의 기본 개념과 역사에 대해서 다뤘습니다. 이번글에선 논문에서 제시하고 있는 핵심 내용에 대해서 다뤄보고자 합니다. 전체적으로 생소한 용어를 사용합니다. 아래 글을
xoft.tistory.com
이번글 3부에서는 COLMAP SfM논문 Structure-from-Motion Revisited (CVPR 2016) 에서 제안하는 나머지 2가지 전략 Bundle Adjustment와 Redundant View Mining에 대해 다루겠습니다.
4. Bundle Adjustment

전체 flow상에 Bundle Adjustment(BA)가 어떤 역할을 하는지에 대해선 1부글 참조 바랍니다. Bundle Adjustment를 통해 카메라 parameter(=카메라 pose)와 3D point를 최적화합니다.
2-2), 2-3) 단계를 1번 수행하면 local한(부분적인) 영역에 대해서만 처리되기 때문에, 항상 global하게 BA를 실행하지 않습니다. 때문에 most-connected(가장 연결성이 높은) 이미지 집합에 대해서만 local BA를 수행합니다. VisualSFM과 유사하게 특정 percentage를 만족시에 global BA를 수행하는 전략을 취했습니다.
Parameterization
카메라 pose에 관한 parameter를 어떻게 설계했는지에 대해 먼저 다루겠습니다.
- outlier를 다루기 위해 robust loss 함수인 cauchy function(이전글)을 적용했습니다. 구체적으로 백여개 카메라 포즈 추정에 대해선 sparse direct solver를 사용하고, 그 이상의 카메라 갯수의 포즈 추정에 대해선 iterative solver인 PCG(preconditioned conjugate gradients)를 사용했습니다.
- 또한 Ceres Solver를 사용하였고 어떤 복잡한 카메라 parameter도 여러 이미지 간에 공유할 수 있도록 옵션을 만들었습니다.
- 정렬되지 않은 인터넷 사진들에 대해선 하나의 radial distortion parameter로 카메라 parameter를 모델링했고, self-calibration으로 이 parameter를 추정했습니다.
Filtering
추정된 카메라 모델(=카메라 parameter)에 적합하지 않은 case가 발생하게 되는데 이를 위해 reprojection error가 큰 경우에 대해 filtering을 수행합니다.
- 모든 카메라쌍으로 ray를 그려 최소 triangulation 각도를 갖는지를 보며 well-condition된 geometry인지를 확인하여 필터링합니다.
- Global BA(모든 카메라 parameter refinement)이후엔, panorama나 인위적으로 수정된 이미지로 인해 발생된 카메라 에러 케이스가 있는지를 확인하여 필터링합니다.
- 일반적으로 카메라는 외부 관측(outlier observations)만 존재하거나 내부 파라미터(intrinsics)가 잘못된 최소값(bogus minimum)으로 수렴하는 경향이 있습니다. 때문에 카메라 focal length와 distortion parameters를 사전에 고정된 범위로 제한하지 않고, 번들 조정(Bundle Adjustment, BA) 중 자유롭게 최적화되도록 합니다.
- 카메라 principal point 보정은 ill-posed problem로 알려져 있기 때문에, 보정되지 않은(uncalibrated) 카메라에서는 principal point를 이미지 중심에 고정시킵니다. 비정상적으로 넓은 Fov(field of view)를 가지거나 왜곡 계수의 크기가 큰 카메라는 잘못 추정된 것으로 간주하여 필터링합니다.
Re-Triangulation
VisualSfM과 유사하게, global BA 전에 drift 효과를 보정하기 위해 re-triangulation를 수행합니다. 논문에선 Pre-BA RT라고 부르고 있습니다.
- BA 수행 시 카메라와 point parameter값이 크게 되는 경우가 발생되는데, Pre-BA RT를 통해 이를 보정하게 됩니다.
- triangulate에 실패하는 point들 추적을 통해 reconstruction의 completeness를 향상시킵니다. triangulation thresholds을 이상인 값을 추적하는 대신 filtering threshold 를 초과하지 않는 point들을 추적합니다.
- track을 merge하여 다음 BA단계에서 이미지간 point 중복성을 가지도록 합니다.
Iterative Refinement
Bundler와 VisualSfM연구에서는 BA와 filtering을 단일 단계로 진행하지만, drift나 pre-BA RT로 인해서 많은 observation이 필터링되어 사라집니다. BA가 outlier에 상당한 영향을 미치기 때문에, BA의 두번째 단계에선 상당한 성능 개선이 이뤄지게됩니다. 때문에 filtered된 observation갯수와 post-BA RT point 갯수가 줄어들 때까지 BA, RT, filtering을 iterative하게 optimization수행합니다.
5. Redundant View Mining

BA는 연산량이 많아서 전체 pipeline에서 bottleneck이 됩니다. 이를 해결하기 위해 논문에서는 incremental SfM의 특징을 이용하는 방법을 제안합니다. 장면 중복도가 높은 카메라들을 클러스터링하여 효율적인 BA parameterization 방법에 대해 제안하고 있습니다.
일반적으로 한개 scene 촬영시 사진을 촬영한 위치는 균일한 분포를 갖지 못합니다. 공통적으로 촬영된 영역을 통해서 이미지 클러스터가 만들어지게 됩니다. 이러한 특징을 활용한 연구 3가지는 다음과 같습니다.
- Kushal et al. [33] : 카메라 시스템을 효율적으로 전처리하기 위해 visibility 패턴을 분석했습니다.
- Ni et al. [43] : separator variable을 통해 연결된 카메라-point graph를 submap으로 분할 후 graph cut문제로 정의해서 연결 관계를 최적화했습니다. "카메라와 포인트 파라미터를 고정한 상태에서 Separator Variables를 최적화"하는 방식과 "Separator Variables를 고정한 상태에서 카메라와 포인트를 최적화"하는 방식을 번갈아가면서 수행했습니다.
- Carlone et al. [11] : 다수의 point를 저차원으로 압축하면서 계산하고, camera는 고차원으로 늘여 계산하는 방식을 제안했습니다. point의 차원을 축소하면서 카메라가 많은 점을 공유하는 케이스에서 계산 효율성을 갖게 했습니다.
본 연구에서는 Ni et al. [43]기법과 유사하게 submap으로 분할하였고, submap 내부 parameter는 따로 추출하여 독립적으로 처리했습니다. 본 연구의 기여포인트 3가지를 먼저 언급하고 있습니다.
- Ni et al. [43] graph cut를 효율적인 다른 방식으로 대체하였습니다.
- Ni et al. [43]에선 많은 카메라를 하나의 submap으로 묶었지만, 본 논문에서는 겹침이 많으면서 작은 갯수를 가지도록 카메라 그룹으로 장면을 분할 했습니다. 각 그룹 내 카메라들을 하나의 single 카메라 parameter로 모델링하여 계산량을 줄여줬습니다.
- 겹침이 많으면서 작은 갯수를 가지는 카메라 그룹 consequence를 사용해서 Ni et al.[43]의 alternation scheme(교차 최적화 방식)을 제거하고 동시에 separator 최적화 과정을 생략하여 계산 효율을 높였습니다.
다음으로 본 연구의 구체적인 알고리즘입니다.
인터넷에서 수집된 이미지들의 카메라 포즈는 고르게 분포되지 않고 중복된 viewpoint가 몰려있는 경향이 있습니다. 이를 구분해서 처리하기 위해, 직전에 수행된 incremental model extension에 의해 이미지와 point가 영향을 받았는지 여부에 따라 두 집합으로 나눕니다. 1) 새롭게 확장된 영역을 중심으로 최적화가 수행하는 집합과 2) 그 외 영역에서는 drift(누적 오차)가 발생한 경우 업데이트하는 집합으로 나눌 수 있습니다. 대규모 이미지 입력이 주어질 경우 모델은 local extension이 되기 때문에 대부분의 scene은 영향 받지 않고 그대로 유지됩니다.
- 집합2) 영향 받지 않은 scene part에 대해 highly overlapping images들을 각각 그룹들 $g = \{G_r | r = 1...N_G\}$으로 구성합니다. 각 그룹 $G_r$은 single 카메라 parameter로 설계했습니다. 영향 받지 않은 이미지들은 그룹 크기 $N_{G_r}$로 생성됩니다.
- 집합1) 직전에 수행된 extension과 관련된 이미지들을 따로 refinement하기 위해 독립적으로 그룹화합니다. 다음 두 조건 중 하나를 만족하면 영향을 받은(affacted) 것으로 간주합니다. (1) 해당 이미지가 최근의 model extension에 추가된 경우와 (2) 이미지 observation의 일정 비율 이상이 reporjection error가 r pixel보다 큰 경우에 추가됩니다.
그 후 표준 BA parameterization을 수행합니다. 수식 설명은 1부 가장 아래에 있습니다. $$ E = \sum_j \rho_j \left( \| \pi(P_c, X_k) - X_{j} \|_2 \right)^2 $$ 글 흐름상 그룹별로 BA를 수행하는 것 같은데 정확히 표현되어 있지 않습니다.
공통적으로 관측되는 점 갯수를 기반으로 중복되는 이미지들이 그룹화 되도록 만듭니다. $N_x$개 point를 가지는 하나의 scene에서 각 이미지들은 0과1로 visibility를 표현하는 벡터인 binary visibility vector로 설계 할 수 있습니다. 이미지에서 공통으로 보이는 점이면 1이고 안보이면 0입니다. 이미지 a와 이미지 b의 관련성 계산을 다음의 bit연산으로 설계했습니다. $$ V_{ab} = \frac{\|\mathbf{v}_a \wedge \mathbf{v}_b\|}{\|\mathbf{v}_a \vee \mathbf{v}_b\|}. $$
- 이미지들을 아래 수식으로 sorting합니다. $$\overline{I} = \{ I_i \|\mathbf{v}_i\| \geq \|\mathbf{v}_{i+1}\| \}$$ $\overline{I}$에서 첫번째 image $I_a$에 대해 group $G_r$에 넣습니다.
- $V_{ab}$를 최대화하는 image $I_b$를 찾습니다. $V_{ab} > V$ 이고 $\ |G_r| < S$이면 이미지 $I_b$는 group $G_r$에 추가됩니다.
- 위 조건에 충족되지 않는다면, 해당 $I_b$는 새로운 그룹의 첫번째 image로써 추가됩니다.
- $I_b$를 찾는 시간을 줄이기 위해서, 시야 방향이 ±$\beta$도 범위 내에 있는 $K_r$개의 공간적으로 가까이에 있는 이웃을 탐색하도록 휴리스틱하게 적용했습니다.
- 하나의 그룹안에 각 이미지는 공통된 group-local 좌표계(특정 좌표계)의 매개변수로 정의하였습니다.
그룹화된 이미지들의 BA cost function은 $$ E = \sum_j \rho_j \left( \| \pi(G_r, P_c, X_k) - X_{j} \|_2 \right)^2 $$ 이 됩니다. 기존 수식에서 extrinsic group parameters $G_r \in SE(3)$가 추가되었습니다. group r 내 이미지의 projection matrix는 group과 이미지 pose의 행렬곱 $P_{cr} = P_cG_r$ 으로 정의됩니다.
전체 비용 $\overline{E}$는 그룹화된 비용과 비그룹화된 비용 기여도의 합으로 정의했습니다. $G_r$와 $P_i$의 회전 성분을 효율적으로 다루기 위해 쿼터니언 표현법(이전글)을 사용했습니다. 그룹 크기가 커질수록 더 큰 성능 이점을 얻을 수 있었다고합니다. $\pi$에 비해 $\pi_g$를 계산하는 것이 상대적으로 오버헤드를 작아지게 했기 때문이라고 합니다. (마지막 문장은 이해가 안되는 부분입니다.)
추가적으로, 성능의 이점은 문제의 크기에 따라 달라집니다. 카메라 수를 줄이게 되면 직접 방식(direct methods)의 세제곱 복잡도에 더 큰 영향을 미치는 반면, 간접 방식(indirect methods)의 선형 복잡도에는 상대적으로 적은 영향을 미친다고 합니다.
Experiment
총 144,953장의 순서 없는 인터넷 사진들로 구성된 17개의 데이터셋을 사용했습니다. 이 사진들은 넓은 영역에 분포되어 있고, 카메라 밀도 또한 매우 다양합니다. Quad [14] 데이터셋의 경우, 카메라 위치 GT데이터를 포함하고 있습니다. 모든 실험에서 RootSIFT 를 사용했고, 각 이미지는 별도의 데이터셋에서 학습된 vocabulary tree를 기반으로 가장 가까운 100개의 이웃 이미지와 매칭했습니다. 수행시간 비교시 correspondence search시간을 제외하고, 2.7GHz CPU에 256GB RAM을 사용했습니다.
Next Best View Selection

점의 개수와 분포를 얼마나 잘 반영하는지 평가하기 위해 (2부에서 2절에서 언급된) score S 를 사용합니다. L = 6개의 피라미드 레벨을 사용하며, 분산 $\sigma$와 위치 $\mu$를 가진 Gaussian 분포의 이미지 점들을 생성합니다. $\sigma$가 커지고 $\mu$가 중앙에 가까워질수록 분포가 더욱 균일해지며, 이로 인해 더 높은 점수를 생성합니다. 마찬가지로, 점수가 적을 때는 점의 개수가 점수에 더 큰 영향을 미치며, 점의 개수가 많아지면 점의 분포가 점수에 현저히 영향을 미칩니다.

재구성 오류 측면에서 제안하는 본 연구의 pyramid방법과 이전 연구들을 비교합니다. 이전 연구의 삼각화된 점의 개수를 최대화하는 Number기법과, 잠재적으로 보이는 점 대비 실제로 보이는 점의 비율을 최대화하는 Ratio기법을 비교하였습니다.
각 이미지 registration 이후, 본 논문에서는 전략 간에 공유되는 register된 이미지의 개수(=intersection over union)와 재구성 오류(카메라위치에 대한 GT와 예측 거리=median error)로 측정합니다. 기존 연구들은 등록된 동일한 이미지 집합으로 수렴했지만, 본 연구에선 이미지를 registration 정렬 기반으로 선택하여 정확한 reconstruction을 만들어냈습니다.
Robust and Efficient Triangulation
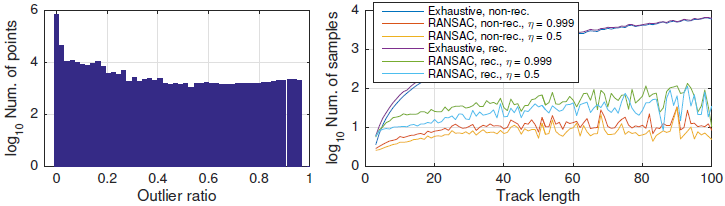
4700만 개의 검증된 매칭으로 구성된 290만 개의 특징 트랙(feature tracks)을 가진 Dubrovnik 데이터셋으로 평가했습니다. Bundler와 트랙 내 모든 쌍별 조합을 샘플링하는 완전 탐색(exhaustive) 전략과 비교했습니다.
실험에서는 $\alpha = 2^\circ$, $t=8px$, $\epsilon_0 = 0.03$으로 설정했습니다. combinatorial explosion을 방지하기 위해 완전 탐색 접근법의 반복 횟수를 10,000번으로 제한하며, 이 경우 $\epsilon_{\text{min}} \approx 0.02$, $\eta = 0.999$로 설정했습니다. (재귀적이고 완전 탐색적인 접근법으로 측정된) 다양한 inlier 비율 분포는 robust triangulation 방법의 필요성을 보여주고 있습니다.
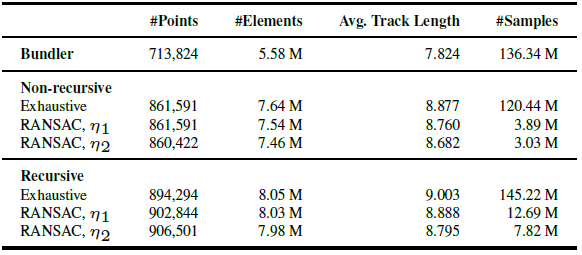
본 논문에서 제안된 recursive 접근법은 non-recursive 방법에 비해 상당히 더 긴 트랙과 더 많은 트랙 요소를 복원했습니다. 재귀적 RANSAC 기반 방법에서 점(point)의 개수가 더 많아지면서 트랙 길이가 약간 줄어드는 것을 볼 수 있습니다.
RANSAC 기반 접근법은 약간 짧은 트랙을 생성하지만, 속도 면에서는 훨씬 빠르며(10-40배) 더 효율적입니다.
$η$값을 조정하면 속도와 completeness간의 균형을 쉽게 맞출 수 있습니다. 위 표에서 $η_1$은 0.99, $η_2$는 0.5입니다.
Redundant View Mining

밀집하게 분포된 이미지들의 순서 없는 컬렉션에서 중복 뷰 탐색을 평가했습니다. 위 그림은 고정된 BA 반복 횟수를 사용하는 경우, 전역 BA에서 파라미터화된 카메라의 growth rate을 보여줍니다. scene overlap 비율 V에 따라, reduced 카메라 시스템에서 BA 수행 시간을 크게 줄일 수 있습니다. 전체 실행 시간의 유효 속도 향상은
V=0.6일 때 5%,
V=0.3일 때 14%,
V=0.1일 때 32%입니다. 평균 재투영 오차는 표준 BA(0.26px)에서 각각 0.27px, 0.28px, 0.29px로 약간 증가했습니다.
reconstruction quality는 V>0.3인 경우 모두 비슷한 수준으로 유지됬으며, V 값이 더 작아질수록 점점 더 하락됬습니다. V=0.4를 사용할 경우, Colosseum 데이터셋의 전체 파이프라인 실행 시간이 36% 감소하지만, 여전히 동등한 수준의 reconstruction 결과를 볼 수 있었습니다.
System


전체 시스템 개별 구성요소에 따른 평가입니다.
Theia는 가장 빠른 방법이며, 본 연구는 VisualSFM보다 약간 느린 시간이 소요되지만 Bundler보다는 50배 이상 빠릅니다.

위 그림은 각 모듈의 상대적인 실행 시간을 보여줍니다.
모든 데이터셋에서, 특히 더 큰 모델에 대해, 본 연구는 completeness 측면에서 다른 어떤 방법보다 훨씬 더 우수한 성능을 보입니다. 중요한 포인트는, 트랙 길이가 증가함에 따라 BA에서 더 높은 중복성(redundancy)이 발생했다는 점입니다.
추가적으로, Quad 데이터셋에서 best pose accuracy를 달성했습니다:
- DISCO: 1.16m
- Bundler: 1.01m
- VisualSFM: 0.89m
- Ours: 0.85m

위 그림은 Bundler(왼쪽)와 본 연구(오른쪽) 방법을 비교한 결과입니다. 본 연구가 뛰어난 robustness, completeness, accuracy을 갖추고 있음을 보여줍니다.
Closing..
논문을 정확히 이해하고 리뷰 글을 작성했다면 매끄러웠을텐데, 그렇진 못해서 뒤로 갈수록 글이 많이 딱딱해지는 경향이 있네요. 요약 정리하는 글로 마무리하고 싶지만 섣부른 이해도로 정리하기엔 잘못된 정보를 전달 할 것 같아 여기서 글을 마치겠습니다. 긴글을 여기까지 끝까지 읽으신 분들께 끝까지 읽어주셔서 감사하다는 말남깁니다. image matching, 비선형 최적화, RANSAC, 카메라 모델 등 다양한 개념을 알고 있어야 읽을 수 있는 논문이라 진입장벽이 있네요. COLMAP을 매번 라이브러리 형태로 가져다 쓰는 입장에서 동작 원리가 궁금해서 리뷰를 해보았습니다. 부족한 글이지만 개념 파악에 도움이 되었으면 합니다.
'Camera Model' 카테고리의 다른 글
| [개념 정리] SfM(Structure from Motion) of COLMAP - 2부 (5) | 2025.01.05 |
|---|---|
| [개념 정리] Quaternion (쿼터니언) 회전 (0) | 2024.12.23 |
| [개념 정리] Rotation Matrix (회전 행렬) (1) | 2024.12.21 |
| [논문 리뷰] MASt3R (arXiv2024) : 3D기반 Image Matching 기법 (5) | 2024.06.30 |
| [개념 정리] Fronto Parallel Plane (0) | 2024.05.26 |




댓글