Rotation Matrix는 2D 및 3D 공간에서 3D모델 또는 카메라 회전을 수행하는 데 사용됩니다.
Euler Angle
Rotation matrix는 오일러 각(Euler Angle)을 기반으로 합니다. 물체의 회전을 나타내는 방법중에 하나입니다. (그림 : link)
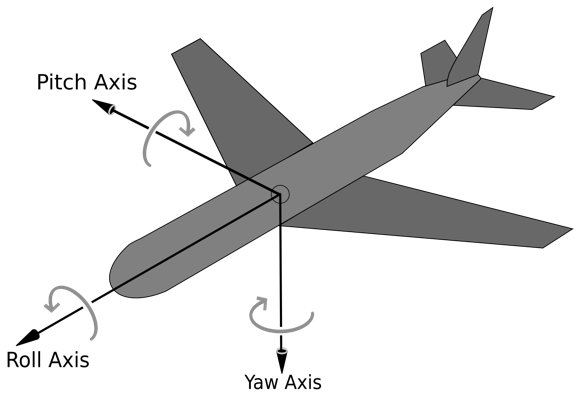
x, y, z 각 축을 기준으로 회전하는 각도를 사용합니다.
2D Rotation Matrix
2D에서 원점을 기준으로 각도 만큼 반시계 방향으로 회전시키는 행렬입니다. $$ R =
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix} $$
Rotation Matrix으로 point (x,y)를 회전하는 수식은 아래와 같습니다.

점 (1,0)을 시작으로 θ가 10도씩 증가하는 예시입니다.
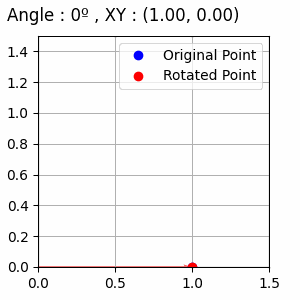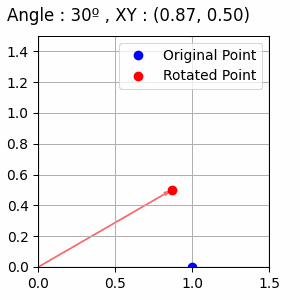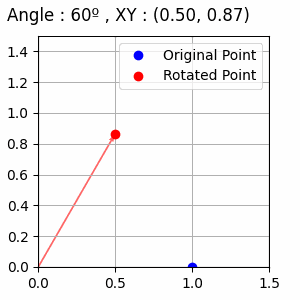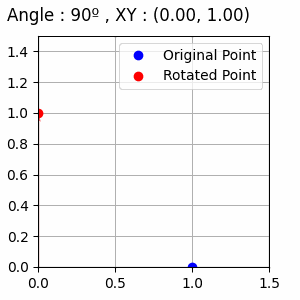
코드입니다.
import numpy as np
def rotate_2d(point, angle_degrees):
angle_radians = np.radians(angle_degrees)
rotation_matrix = np.array([
[np.cos(angle_radians), -np.sin(angle_radians)],
[np.sin(angle_radians), np.cos(angle_radians)]
])
return np.dot(rotation_matrix, point)
3D Rotation Matrix
3D에서 원점을 기준으로 각 축을 각도 만큼 반시계 방향으로 회전시키는 행렬입니다.
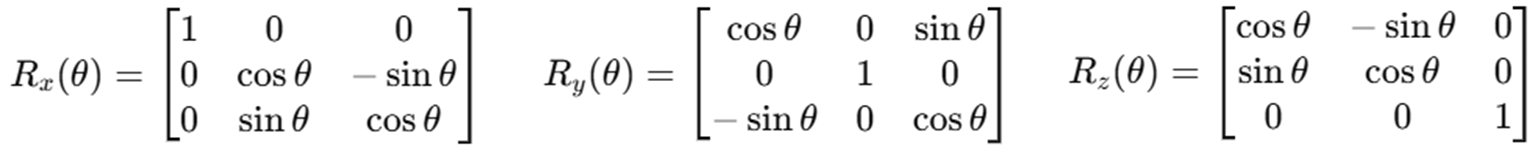
위 3개 행렬을 곱하면, 3개 축에 대해서 회전이 가능하며, 일반적으로 3개 모두 곱한 것을 3D Rotation Matrix로 부릅니다.
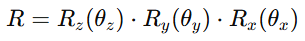
point (x,y,z)를 회전하는 수식입니다.

점 (1,0,0)을 시작으로 $θ_y$(왼쪽 그림), $θ_z$(오른쪽 그림)을 10도씩 증가시킨 예제입니다.
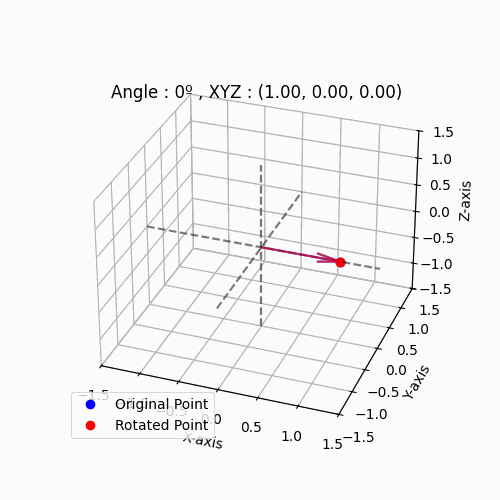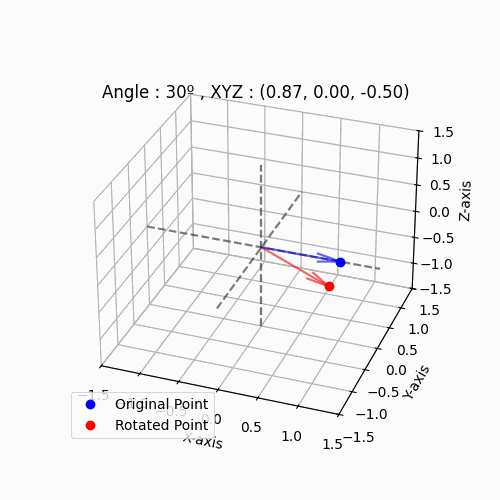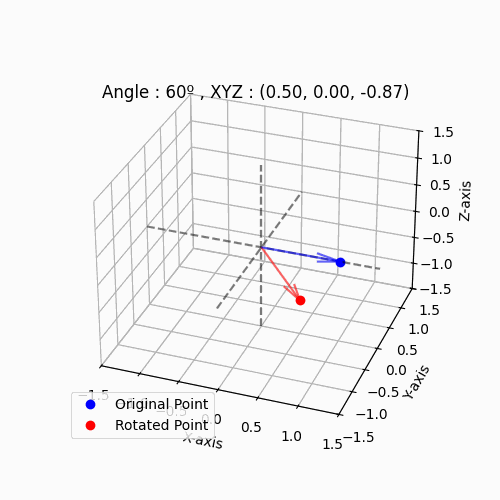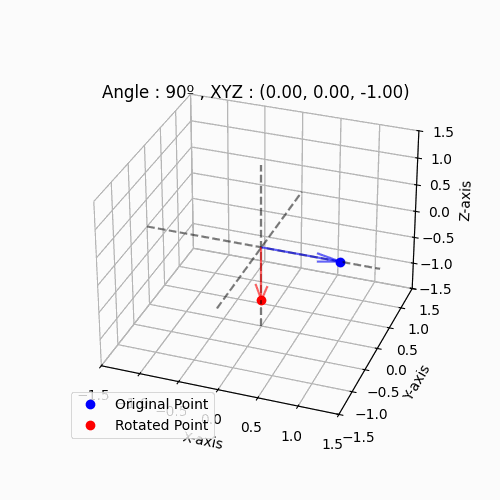 |
 |
코드입니다.
import numpy as np
def create_rotation_matrix_from_euler(yaw, pitch, roll):
R_x = np.array([
[1, 0, 0],
[0, np.cos(roll), -np.sin(roll)],
[0, np.sin(roll), np.cos(roll)] ])
R_y = np.array([
[np.cos(pitch), 0, np.sin(pitch)],
[0, 1, 0],
[-np.sin(pitch), 0, np.cos(pitch)] ])
R_z = np.array([
[np.cos(yaw), -np.sin(yaw), 0],
[np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1] ])
return R_z @ R_y @ R_x # ZYX 순서로 곱셈
roll,pitch,yaw = np.radians(20), np.radians(30), np.radians(40)
rotate_matrix = create_rotation_matrix_from_euler(roll,pitch,yaw)
point = (1,0,0)
rotated_point = np.dot(rotate_matrix, point)
코드를 보면, degree -180~180 범위가 아닌 radian -$\pi$ ~$\pi$ 범위로 바꿔 계산합니다. 그리고 python에서 행렬연산은 @ 연산자로 할 수 있습니다. 행렬연산은 dot 연산으로도 할 수 있습니다. point 회전시엔 dot을 쓰는 예시를 넣었습니다.
$R_x$, $R_y$, $R_z$ 곱하는 순서에 따라 결과가 달라집니다.
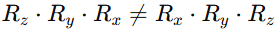
항공우주 및 로봇 공학에서는 Roll(x축), Pitch(y축), Yaw(z축)용어를 쓰기 때문에, x->y->z순으로 회전하기 위해서 $R_z$, $R_y$, $R_x$순으로 사용하고, 컴퓨터 그래픽에서는 ZYX순으로 쓰기도 하지만 XYZ순으로 쓰기도 합니다.
(기본 개념은 여기까지입니다. 더 자세한 개념을 파악하고 싶으신 분은 추가로 읽으시면 됩니다.)
Rotation Inverse Matrix (역행렬)
회전된 점(x',y',z')에서 원래 점(x,y,z)으로 되돌아가기 위해서 필요합니다. 반대 방향의 회전이기 때문에, 30도 회전의 역행렬은 -30도 회전과 동일합니다.
회전행렬은 행(=x)과 열(=y)이 서로 직교하는 orthonormal matrix(정규 직교 행렬)의 특성을 가지기 때문에, 해당 행렬의 특성 $A^T A = I$ 에 의해(I는 단위행렬), $A^{-1}=A^T$이 되며, rotation matrix의 역함수는 transpose Matrix(전치행렬)가 됩니다.

간단한 증명 방법으로, Rotation matrix에 -θ를 넣어주면 역함수가 만들어집니다.
2D Rotation Matrix를 Inverse Matrix로 만드는 예시입니다.
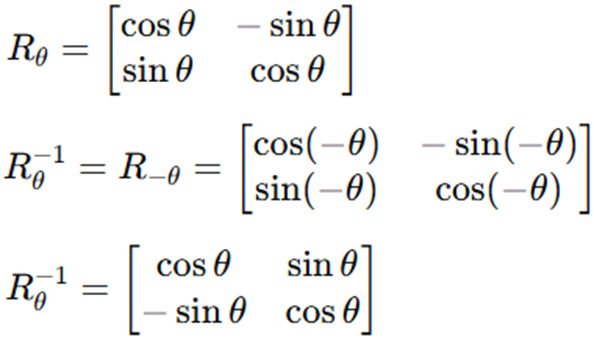
3D Rotation Matrix와 Inverse Matrix입니다.
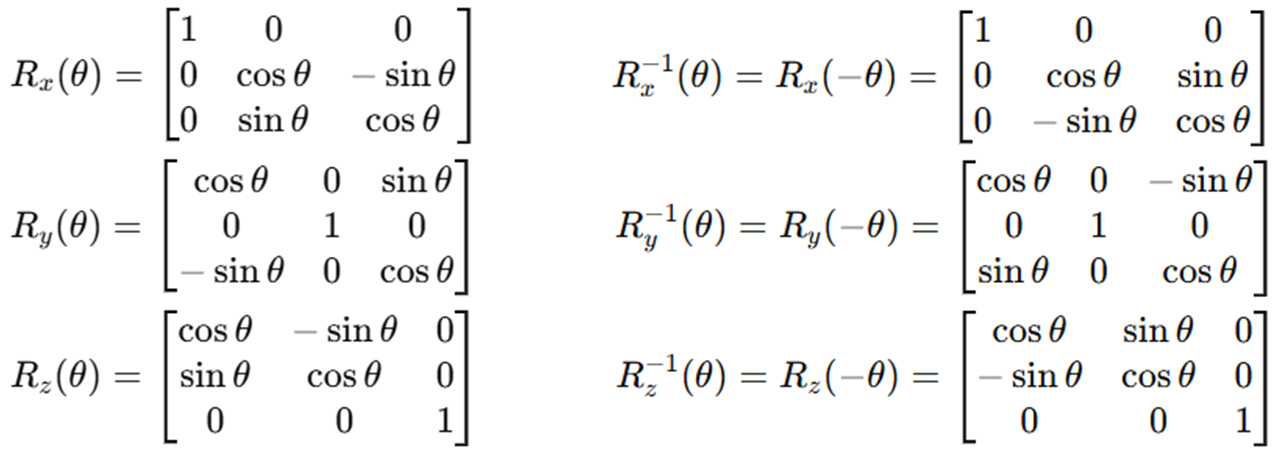
코드는 numpy 함수로 간단하게 작성됩니다.
inverse_rotation_matrix = np.linalg.inv(rotation_matrix)
Rotation Matrix의 문제점 : Gimbal Lock(짐벌락)
Euler Angle 표현법의 문제점으로 보시면됩니다. 위에서 보듯이 3개 각축이 순차적으로 행렬연산이 됩니다. 이 때 두개의 회전축이 겹쳐지면서, 의도하는 각도로 회전되지 않는 현상입니다. 아래 그림(더보기 클릭)은 z,y,x축이 순서대로 회전하는 것을 보여주는 그림입니다. 문제는 초록축 회전시 분홍축과 겹쳐지면서 초록축이 분홍축과 같이 움직이게 된다는 점입니다. (그림 출처 : link)
수식적으로 생각하자면, 먼저 수행한 행렬연산 후의 특정값이 0으로 만들어지면서, 이후에 수행되는 행렬 연산에서 회전에 관련한 값이 0과 곱해지게 되고, 이를 통해 (먼저 수행한 축과 같이 움직이게 되거나) 회전 되지 않게 된다고 볼 수 있습니다.
2D Rotation Matrix에서 각도 θ 추출
Rotation Matrix를 보게되면, 무슨 숫자인지 직관적으로 알 수가 없습니다. 아래는 Rotation Matrix에서 각도 θ를 추출하는 수식입니다.

함수는 x와 y의 부호를 고려하지 않아 각도가 잘못 계산될 가능성이 있습니다. 이를 해결하기 위해 0으로 나누는 오류를 방지하는 arctan2 함수가 사용됩니다.

코드입니다.
import numpy as np
def extract_angle_from_2d_rotation_matrix(R):
if R.shape != (2, 2):
raise ValueError("Input must be a 2x2 matrix.")
angle = np.arctan2(R[1, 0], R[0, 0]) # theta = atan2(sinθ, cosθ)
return angle
3D Rotation Matrix에서 각도 θx, θy, θz 추출
축별 rotation matrix를 곱하는 순서 ZYX순 XYZ순에 따라 다릅니다. 여기선 많이 사용하는 ZYX순을 기준으로 적어봤습니다.

코드입니다.
import numpy as np
def extract_euler_angles_from_3d_rotation_matrix(R):
yaw = np.arctan2(R[1, 0], R[0, 0])
pitch = -np.arcsin(R[2, 0])
roll = np.arctan2(R[2, 1], R[2, 2])
return yaw, pitch, roll
해당코드는 짐벌락문제로 인해 제대로된 결과를 만들어 내진 않습니다.
짐벌락을 해결하기 위한 방법으로, 물체의 회전을 나타내는 다른 방법 중에 하나인 'Quaternion(쿼터니언) 회전'이 주로 사용됩니다. 별도의 글로 다루겠습니다.
'Camera Model' 카테고리의 다른 글
| [개념 정리] SfM(Structure from Motion) of COLMAP - 2부 (5) | 2025.01.05 |
|---|---|
| [개념 정리] Quaternion (쿼터니언) 회전 (0) | 2024.12.23 |
| [논문 리뷰] MASt3R (arXiv2024) : 3D기반 Image Matching 기법 (5) | 2024.06.30 |
| [개념 정리] Fronto Parallel Plane (0) | 2024.05.26 |
| [개념 정리] Bundle Adjustment (1) | 2024.05.16 |





댓글