Likelihood (이전 글 참조) 는 확률 분포가 가정된 상황에서 관측값이 가지는 확률값을 의미합니다.
Maximum Likelihood Estimation(MLE)는 관측되는 데이터들을 가장 잘 모델링하는 확률분포의 parameter를 찾는 알고리즘입니다.
위 2문장으로 Maximum Likelihood Estimation 이 간략하게 설명 됩니다. 아래는 세부적으로 어떻게 계산하는지에 수식적으로 궁금할 경우 읽기 바랍니다.
다양한 확률분포에 대해 예시(Exponential Distribution, Gaussian Distribution, Normal Distribution)를 들며, 어떻게 확률 분포의 parameter를 찾아가는지 다뤄보겠습니다. 이번 글을 읽으면 Text to Image 생성 모델인 Diffusion Model 에서 Gaussian Distribution 부분을 이해하는데 도움이 됩니다. (아래 설명에 모르는 단어 또는 수식이 있다면, 이전 Likelihood 개념 정리글 에서 찾아 보시길 바랍니다.)
예시를 드는 확률 분포의 공통점에 대해 먼저 언급하자면,
- 관측값(x) 를 입력으로 확률값(y)을 출력하는 확률 밀도 함수(pdf)로 정의 될 수 있습니다.
- parameter(θ)를 변수로 두었을 때, peak(정점)를 1개 가집니다. -> 미분 했을 때, 0이 되는 지점이 1개 입니다.
수식을 설명하는 관점에서 다른 점은 Exponential Distribution은 확률 분포 parameter가 1개인 경우이고, Gaussian Distribution은 확률 분포 parameter가 2개 입니다. 1개인 경우부터 먼저 설명하겠습니다.
Exponential Distribution - Maximum Likelihood Estimation

위의 Exponential Distribution은 Event 사이에 시간을 모델링하는 확률 분포로써 사용 될 수 있습니다. 예를 들어, 다른 message를 얻기 위해 얼마나 많은 시간을 기다려야하는지? 다음 사람이 video를 보기 전에 얼마나 많은 시간이 소요되는지?를 모델링 할 수 있습니다.
아래 그림은 위 수식에 대한 확률 밀도 함수(pdf)입니다. λ가 주어진 확률 분포의 parameter입니다. λ의 변화에 따라 관측값 x에 대해 확률값(=Likelihood)이 어떻게 변하는지를 아래 나타냈습니다.
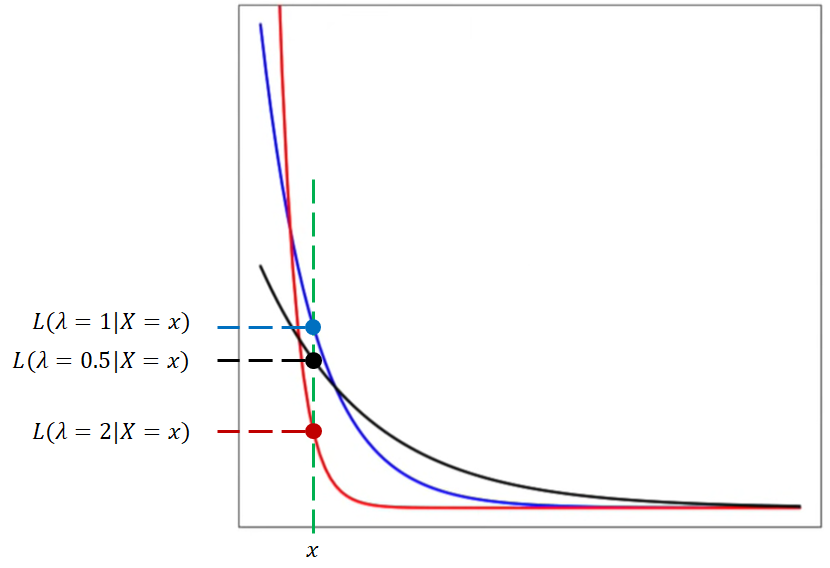
여러 개의 사건이 관측되었을 때, Likelihood(확률)값이 Maximum(최대)가 될 수 있는 λ를 계산해보겠습니다. 여러개 사건이 관측(x)되었을 때, 확률 분포 parameter(λ) 대한 Likelihood에 대한 수학적 정의는 아래 왼쪽 항과 같습니다. 그리고 풀면 4번째 항과 같이 됩니다.

첫번째 우측 항을 먼저 설명하기 위해, 독립 항등 분포(iid : independent and identically distribution)에 대해 알아야 합니다. 확률 분포가 variable에 indepedent(독립적)이고, identically distribution(확률분포가 동일)할 때, iid를 따른다고 합니다. Likelihood를 계산하기 위한 확률 분포들은 iid를 따릅니다. iid는 아래와 같은 특성을 갖기 때문에, 위와 같은 식이 됩니다.
f(x,y,z) = f(x)∙ f(y) ∙f(z)
f(x(1),x(2),…..,x(n)) = f(x1)∙ f(x2) ∙...∙f(xn)
2~4번째 식은 간단한 지수법칙을 사용한 수식이라 생략하겠습니다.
다음 단계로, Likelihood(확률)값이 Maximum(최대)가 되는 λ를 계산해보기 위해, 확률 밀도 함수를 λ에 관한 함수로 그려보겠습니다. x를 3으로 고정하고, λ에 관한 함수로 표현하면 다음과 같습니다.
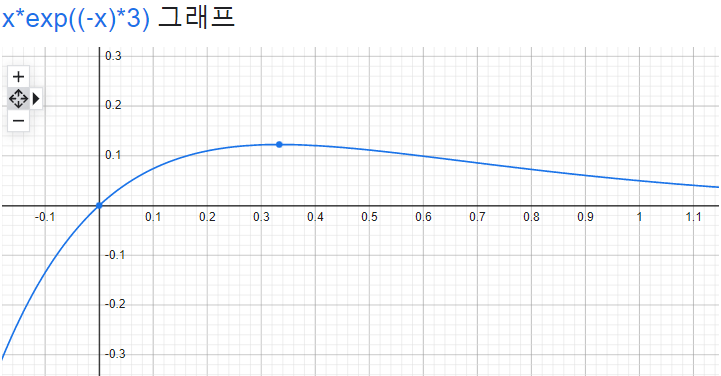
peak가 한개 존재하는 것을 확인해 볼 수 있습니다. 때문에 λ로 미분했을 때 0인 지점을 찾으면, Likelihood의 최대값을 찾는 것을 알 수 있습니다. 위식을 들고 와서 λ로 미분해보겠습니다.

2번째 줄에 log가 붙은 것을 볼 수 있습니다. 미분 했을 때 0인 지점을 찾고 있기 때문에, log를 붙이든 안붙이든 결과는 같습니다. log를 씌워줬을 때, 미분 수식 계산이 용이해지므로 log가 사용되었습니다. 3~5줄도 단순 지수법칙, 로그 성질을 이용하므로 설명을 생략하겠습니다.

1번째 줄은 Likelihood를 미분했을 때 0으로 만들려고 했기 때문에, 넣어준 값입니다. 이를 전개하면, 최종적으로 구하고자 했던 'Likelihood를 Maximum(최대)해주는 확률분포 Parameter(λ)'가 마지막 줄과 같이 계산되어 집니다. 수식을 이해하는데 막히는 부분이 있다면 link 를 참조 바랍니다.
Maximum Likelihood Estimation를 하는 방법에 대해 약간의 감을 잡았을 것이라 생각됩니다. 다음으로 확률분포의 parameter가 2개인 경우를 다뤄보겠습니다.
Gaussian(=Normal) Distribution - Maximum Likelihood Estimation
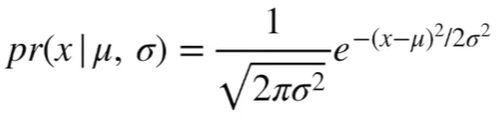
Gaussian Distribution은 Normal Distribution이라고도 불립니다. Maximum Likelihood Estimation에서 많이 쓰는 확률 분포 중에 하나입니다. 자연/사회 과학에서 많이 적용 될 수 있는 확률 분포이며, 관측되는 확률 분포가 평균(μ)과 표준 편차(σ) 형태의 아래와 같은 그래프로 정의 될 수 있을 때 사용합니다. 확률 분포의 parameter가 변화함에 따라 그려지는 그래프는 아래와 같습니다. (그림 출처 : link)

Likelihood(확률)값이 Maximum(최대) 될 수 있는 평균(μ)과 표준 편차(σ)를 계산해보겠습니다. 이번에는 1개만 관측하였을 때, log를 붙여서 풀어보겠습니다. 다시 언급하자면, maximum 값을 구하는 목적에선 log를 씌워도 값이 동일하고, 계산하기가 쉬워진다고 했었습니다.
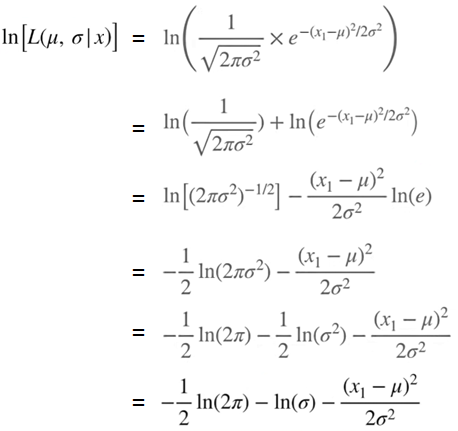
간단한 지수법칙, 로그 성질로 계산 될 수 있습니다. 이렇게 산출된 수식을 여러 개의 관측값이 있는 수식에 대입해보겠습니다. 즉 여러개의 관측값이 존재할 때, Likelihood(확률)값이 Maximum(최대) 될 수 있는 평균(μ)과 표준 편차(σ)를 계산해보겠습니다.
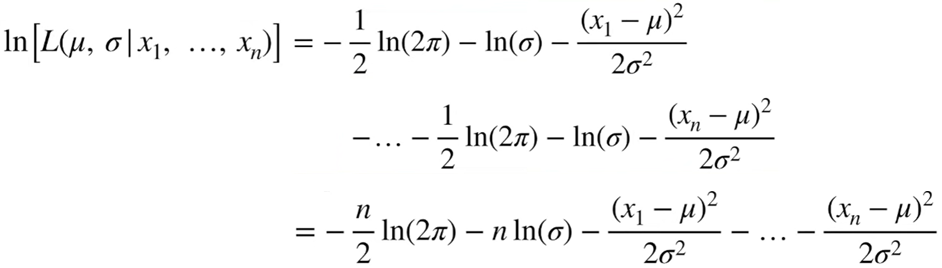
iid(independent and identically distribution)를 따르므로, L( μ,σ | x1, x2, x3 ) = L( μ,σ | x1 ) * L( μ,σ | x2 ) * L( μ,σ | x3 ) 로 변환 될 수 있고, log가 씌워지면서 덧셈 연산으로 바꿀 수 있습니다. 첫번째 줄의 설명이었습니다. 1번째 줄을 정리하면 2번째 줄이 됩니다.
exponential distribution과 동일하게, gaussian distribution를 parameter를 미분하였을 때, 0이 되는 지점이 likelihood가 maximum이 됩니다. gaussian distribution은 변수가 2개(평균(μ)과 표준 편차(σ)) 있기 때문에, 각각에 대해서 편미분 해줍니다. 편미분 했을 때, 0이 되는 지점이 maximum이 될지 확인 해보기 위해서, 각각의 확률분포 parameter에 대해 그래프를 그려보겠습니다.

평균(μ)의 경우 log를 씌웠을 때, 표준 편차(σ)의 경우 log를 씌우지 않았을 때, peak 되는 지점에서 미분이 0이 되는 것을 확인 할 수 있습니다. log를 씌웠을 때와 안 씌웠을 때 교차 가능하기 때문에, 둘중에 한개만 미분이 0이 되는 지점이 최대값인지 확인하면 됩니다. 그럼 각각에 대해 편미분 해보겠습니다.
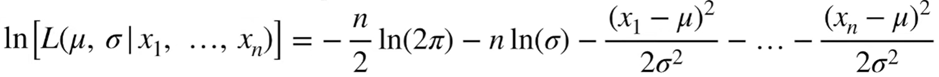

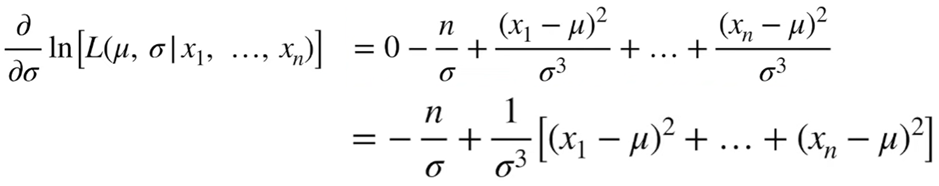
좌항을 0으로 각각 넣어줍니다. 그리고 각각을 전개해줍니다.
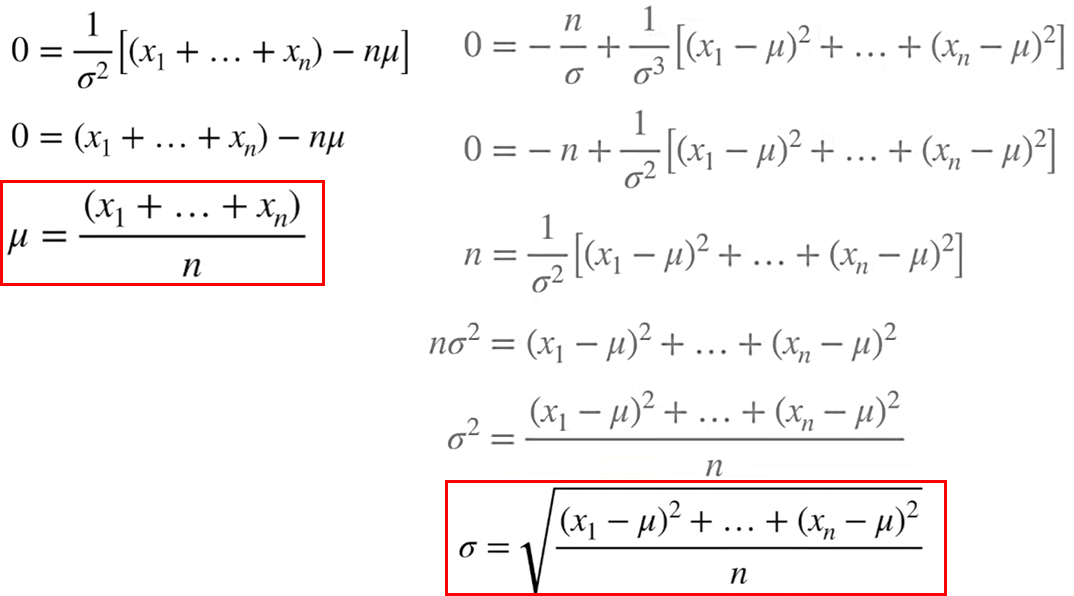
왼쪽은 μ에 대한 식이고 오른쪽은 σ에 대한 식입니다. 빨간색 박스가 최종적으로 찾으려고 한 'Likelihood를 Maximum(최대)해주는 확률분포 Parameter(μ, σ)'에 해당합니다. 수식을 이해하는데 막히는 부분이 있다면 link 를 참조 바랍니다.
마지막으로 한가지 용어 정리를 하고자 합니다. 수식 중간에 언급된 Likelihood에 Log를 씌워주는 것을 Log-Likelihood 라고 합니다. 이 개념에 대해 용어 정리 해보겠습니다.
Log Likelihood
Maximum Likelihood Estimation 시에 계산식을 간단하게 만들기 위해서 Log를 붙여서 사용합니다. Likelihood가 최대(maximum)가 되는 확률 분포의 Parameter를 찾기 때문에, Log를 붙이든 안붙이든 결과는 같습니다. Negative Log Likelihood는 - log ( ) 를 씌워줌으로써, 최대(Maximum)값을 찾는게 아닌 최소(Minimum) 값을 찾는 식이 됩니다.
Closing..
최근 나오는 연구를 읽기 위한 기초를 다지기 위해 글을 작성했습니다. 확률분포가 Gaussian Distribution, Exponential Distribution를 가정하지 않더라도, 위에 언급된 내용을 응용해서 maximum likelihood를 계산 할 수 있길 바랍니다.
출처
Exponential Distribution : link
Normal Distribution : link
iid(independent and identically distribution) : link
'Terminology' 카테고리의 다른 글
| [개념 정리] Marching Cube : 3D Point to Mesh생성 알고리즘 (1) | 2023.08.21 |
|---|---|
| [평가 지표] ATE(Absolute Trajectory Error), RPE(Relative Pose Error) (1) | 2023.05.18 |
| [개념 정리] Likelihood 와 Probability (13) | 2023.03.20 |
| [기술 용어 정리] fidelity 와 quality (1) | 2023.03.11 |
| [개념 정리] Chamfer Distance (0) | 2023.03.08 |




댓글