사전에서 Probability를 '확률', Likelihood는 '가능도, 가능성'라고 합니다. 이 단어의 구별이 잘 되지 않습니다. 한국어로 '확률'은 '어떤일이 일어날 가능성'을 나타냅니다. Likelihood도 '어떤일이 일어날 가능성'을 나타내기 때문에 글의 목적에 따라 Likelihood를 '가능도'라기 보다 '확률'이라고 해석하는게 오히려 번역상 매끄러울 때가 있습니다.
그럼 Probability도 확률이고, Likelihood도 확률입니다. 각각은 어떤 확률을 의미할까요?
- Probability는 주어진 확률 분포가 고정된 상태에서, 관측되는 사건이 변화될 때, 확률을 표현하는 단어입니다.
- Likelihood는 관측된 사건이 고정된 상태에서, 확률 분포가 변화될 때(=확률 분포를 모를 때 = 가정할 때), 확률을 표현하는 단어입니다.
예시를 들겠습니다. 1,2,3,4,5 정수 중에서 특정 값이 관측될 확률을 계산하는 문제가 있습니다.
- 선택 가능한 정수의 범위를 1~5로 제한(확률 분포를 고정)한 상태에서 관측 목표값이 1~5 중에 한개 숫자(관측 되는 사건이 변화)가 될 경우, 확률에 대한 단어를 Probability로 사용합니다. 이 경우 확률값은 0.2로 단순히 계산 할 수 있습니다.
- 선택 가능한 정수의 범위를 1~5가 아닌 다른 정수 범위 1~10 또는 4~50으로 바꾸면서(=확률 분포를 모름), 2가 관측될 확률을 계산(관측 사건이 고정) 할 경우, 확률에 대한 단어를 Likelihood로 사용합니다.
확률 분포가 변화하는 상황에서의 확률(Likelihood)에 대해 좀 더 구체적으로 보겠습니다.
어떤 Task를 반복 수행하는 상황에서, 관측을 n회 했다고 봅시다. Task가 어떤 확률분포를 따른다고 가정을 했을 때, n개의 관측값에 대해 확률값을 가정하며 계산 할 수 있습니다. 이 때의 가정이 들어간 확률이 likelihood입니다. ('~일 것 같은' likely에 명사 어미 '-hood' 로 구성됩니다.) 확률 분포는 다양하게 가정 할 수 있습니다. 분포의 Type을 가정 할 수 있고(첫번째 그림), 특정 Type의 parameter를 다양하게(두번째 그림) 가정 할 수 있습니다. (그림 출처 : link1 , link2)


가정하는 확률값이 의미가 있을까요? likelihood단어는 관측한 데이터를 잘 모델링하는 확률 분포를 찾는 Maximum Likelihood Estimation(MLE) 방법론에서 주로 사용됩니다. (MLE에 대해선 다른 글로 썼습니다. -> link)
아래에선 수식적으로 좀 더 설명하겠습니다.
더 깊게 이해하고 싶으신 분은 선택적으로 더 읽으시면 됩니다. (글이 깁니다...)
Likelihood는 L( θ | x ) 로 표현하고, 같은 의미를 갖도록 Probability로 나타낼 경우 P( x | θ ) 으로 표현합니다. "θ"는 확률 분포를 구성하는 parameter를 의미하고, "x"는 관측값을 의미합니다. " | "는 오른쪽 Term이 주어질 경우, 왼쪽 Term이 나올 확률을 의미합니다.
이산 (셀 수 있는) 사건과 연속 (셀 수 있는) 사건을 구분해서 보겠습니다.
이산 (셀 수 있는) 사건
L( θ | x ) 와 P( x | θ ) 는 같은 값을 나타냅니다. 아래와 같이 표현 할 수도 있습니다.

- L( θ | x )는 관측값이 주어질 때, 변화되는 확률 분포에서 주어진 관측값이 나올 확률입니다.
- P( x | θ )는 확률 분포가 주어질 때, 변화되는 관측값이 나올 확률입니다.
확률 분포가 변화되는 상황 일 때 Likelihood로 표현하고, 관측값이 변화되는 상황 일 때 Probability로 표현한다고 볼 수 있습니다.
L( θ | x ) 와 P( θ | x ) 는 다른 값을 나타냅니다. θ, x의 순서를 주의하셔야 합니다.
- L( θ | x )는 관측값이 주어질 때, 변화되는 확률 분포에서 주어진 관측값이 나올 확률입니다.
- P( θ | x )는 관측값이 주어질 때, 변화되는 확률 분포가 나올 확률입니다.
이산 (셀 수 있는) 사건에서 확률값을 계산할 경우, 이산 사건의 확률 분포를 표현하는 함수 중에 확률 질량 함수(=PMF=Probability Mass Function)를 사용합니다. 사건(x)에 대한 확률값(y)로 구성되어 있으며, y는 항상 0이상이고 Σ f(x)가 1인 함수 입니다.아래는 PMF의 예시입니다. (그림 출처 : link)
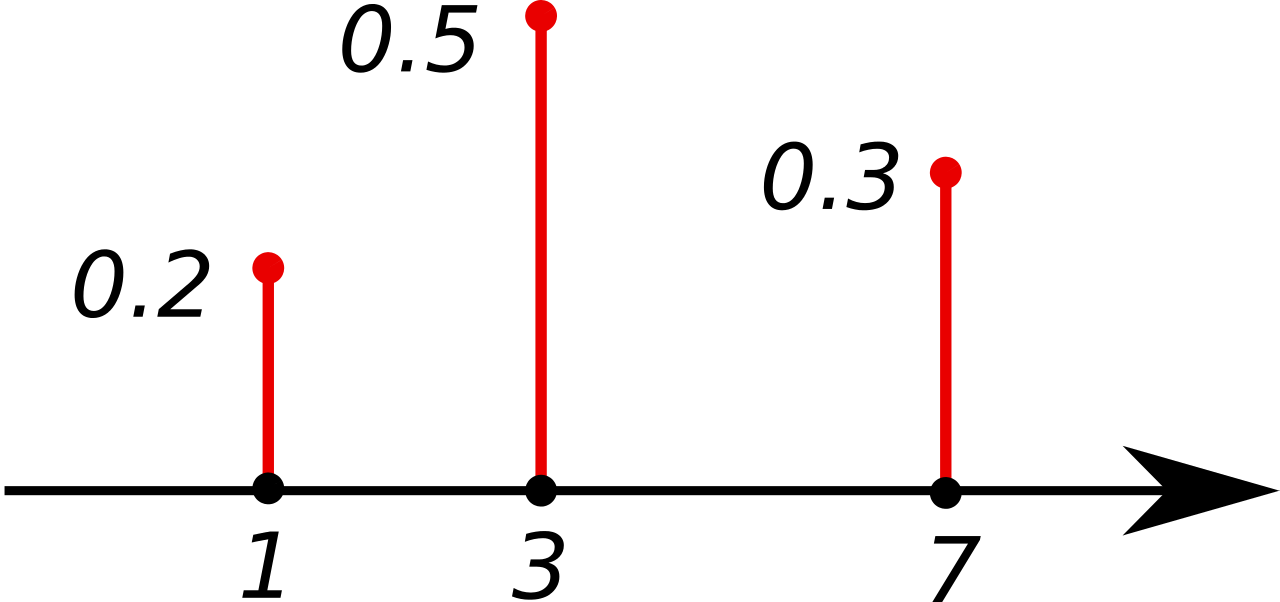
이산 사건에서 확률분포 L( θ | x ) 값은 P( x | θ ) 값을 사용하면 됩니다.
여러 개의 사건이 동시에 발생할 확률은 각 사건에 대해 Probability P( x | θ )의 곱으로 계산합니다.

예를 들어보겠습니다.
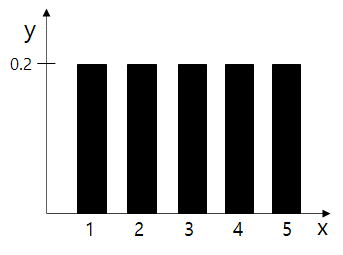
1,2,3,4,5 정수 중에서 2를 관측할 Probability P( x=2 | θ=1,2,3,4,5 )는 0.2 입니다. (확률 분포 범위가 고정되어 있고 관측값을 변화시키는 상황에서 해당 단어가 사용됩니다.)
1,2,3,4,5 정수 중에서 2를 관측할 Likelihood L( θ=1,2,3,4,5 | x=2 )은 0.2 입니다. (확률 분포 범위를 모르는 상황에서 해당 단어가 사용됩니다.)
1,2,3,4,5 정수 중에서 2,5를 관측할 Probability P( x=2,5 | θ=1,2,3,4,5 )는 0.2*0.2=0.04입니다.
1,2,3,4,5 정수 중에서 2,5를 관측할 Likelihood L( θ=1,2,3,4,5 | x=2,5 )는 0.2*0.2=0.04입니다.
연속 (셀 수 없는) 사건
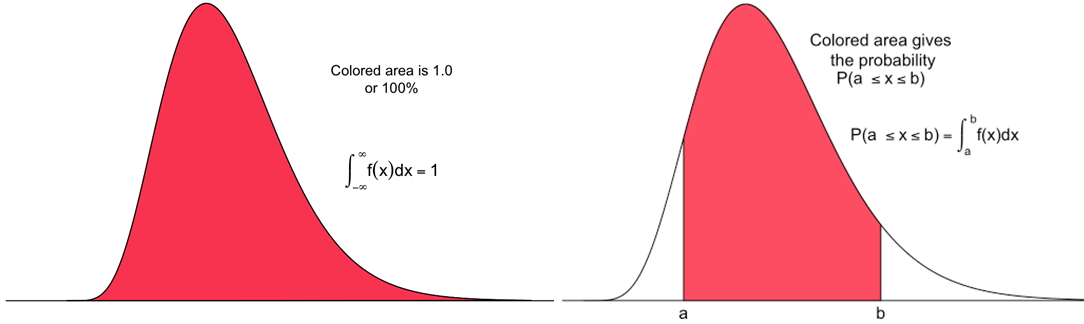
연속 사건의 확률 분포를 표현하는 함수 중에 하나로써, 확률 밀도 함수(=PDF=Probability Density Distribution)를 사용합니다. 사건(x)에 대한 확률값(y)으로 구성되어 있으며, y는 항상 0이상이고 전체 면적(=적분값)이 1인 함수 입니다. (그림 출처 : link)
이산 사건에서 P( x | θ ) 와 L( θ | x )이 동일 했던 것 과 달리, P( x | θ ) 와 L( θ | x ) 는 다른 값을 가집니다.
Probability P( x | θ ) 계산시, 특정 단일 사건(x)이 발생할 확률이 0 (=1/∞)이기 때문에 사용하지 않습니다.
Likelihood L( θ | x ) 계산시, 특정 단일 사건(x)이 발생할 확률을 확률 밀도 함수(pdf)의 y값으로 사용합니다.
Probability P( x | θ ) 계산시, 사건 범위(x1~x2)가 발생할 확률을 확률 밀도 함수(pdf)의 범위 면적값으로 사용합니다.
Likelihood L( θ | x ) 계산시, 사건 범위(x1~x2)가 발생할 확률은 계산할 수 없습니다.
여러개의 단일 사건들에 대한 Probability P( x | θ )만 아래 식으로 계산 할 수 있습니다.

다시 예를 들어보겠습니다.
1~5 실수 범위에서 2를 관측할 Probability는 0(=1/∞) 입니다.
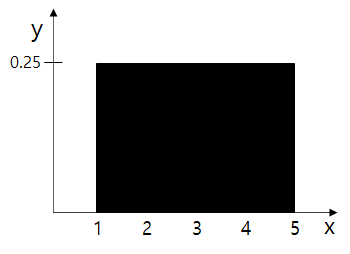
1~5 실수 범위에서 2를 관측할 Likelihood는 0.25 입니다. (확률 밀도 함수(pdf)는 y=0.25 입니다. 0.25는 1/(5-1)로 계산됩니다.)
1~5 실수 범위에서 2~3 실수 범위를 관측할 Probability는 0.25입니다.
다른 예를 들어보겠습니다.
평균(mean = μ)이 0이고, 표준편차(standard deviation = σ)가 1.0인 정규 분포(Normal Distribution)가 확률 분포로 주어질 때, 0.5가 관측 될 확률을 알고 싶습니다. 이 때의 확률은 Probability가 아닌 Likelihood가 쓰이겠죠?
0.5이라는 사건이 관측됬을 때, 평균이 0이고 표준편차가 1.0인 정규 분포에서 해당 사건이 관측될 확률값을 계산하는 문제입니다. 정규 분포의 확률 밀도 함수(pdf)는 다음 수식으로 알려져 있습니다.

Likelihood값은 위 수식에서 x=0.5 , μ=0 , σ=1.0 를 대입하면 됩니다. 아래 확률값을 진한 빨간색으로 표시해두었습니다. 아래 pdf에서 y값이 Likelihood입니다.

Closing..
학생 때, likelihood 개념을 이해했었다고 생각했는데, 글을 정리하면서 이전에 잘못 이해했었구나 싶네요. 다른분께도 도움이 되는 글이길 바랍니다. 다음글은 Maximum Likelihood Estimation(MLE)에 대해서 썼습니다. 관측한 데이터를 잘 모델링하는 확률 분포를 찾는 방법에 관해 수식적으로 다루었습니다.
'Terminology' 카테고리의 다른 글
| [평가 지표] ATE(Absolute Trajectory Error), RPE(Relative Pose Error) (1) | 2023.05.18 |
|---|---|
| [개념 정리] Maximum Likelihood Estimation 와 Log Likelihood (0) | 2023.03.23 |
| [기술 용어 정리] fidelity 와 quality (1) | 2023.03.11 |
| [개념 정리] Chamfer Distance (0) | 2023.03.08 |
| [개념 정리] HDR : High Dynamic Range (0) | 2023.02.05 |




댓글