본 논문에서는 3D Gaussian Splatting(3D-GS, 이전글)으로 생성한 Scene을 3D Mesh로 만드는 방법에 대해 다룹니다.
이 논문을 통해 아래의 것들이 가능하게 됩니다.
- 서로 다른 Scene에서 Reconstruction한 Object들을 높은 퀄리티로 다른 Scene에 배치
- 전통적인 3D 편집툴(Blender, Unity 등)으로 Scene을 Editting, Sculpting(조각), Animating, Relighting
고퀄리티의 재밌는 콘텐츠를 만들 수 있습니다! 서로 다른 왼쪽 3개 Scene에서 오른쪽 1개의 Scene으로 만든 예시입니다.

3DGS-to-Mesh 문제점 & 제시하는 해결방안
[문제점1] 3D-GS의 surface를 mesh로 표현하게 되면, Gaussian들이 구조화되어있지 않아서 Mesh를 추출하기가 어렵습니다.
1) 정렬된 Structure를 갖지 않습니다.
2) 실제 Surface와 일치하도록 모델링하기가 어렵습니다.
[해결방안1] Scene Geometry를 잘 획득하기 위해,
- Scene의 surface에 Gaussian들이 flat하게 잘 배치 할 수 있도록 Regularization Term을 사용했습니다.
- 생성된 Gaussian들로부터 volume density를 획득하고 실제 volume density와 차이를 최소화했습니다.
[문제점2] GS로 만든 scene이 high-fidelity(=높은 재현율, 이전글)을 가지게 하려면, Gaussian의 갯수를 늘여야 합니다. 일반적으로 수백만개의 3D Gaussian으로 만들어지게 되며, scene의 texture와 detail을 표현하기 위해 극단적으로 작은 3D Gaussian들로 구성되게 됩니다. 이렇게 되면 거의 모든 영역에서 density function의 출력값이 0에 가깝게 만들어지며, 이 결과에 Marching Cube알고리즘(이전글)을 사용해서 triangle mesh를 획득 할 경우, fine한 voxel grid에서 적절한 (sparse) density function을 만들 수 없습니다.
[해결방안2] Poisson Reconsturction 알고리즘(이전글)을 통해 triangle mesh를 획득하기 위해 Density Function의 Visible영역에서 효율적으로 point 샘플링하는 기법을 도입합니다. Density Function에서 density 크기별로 level을 설정하여 level set으로 구성하고, 이 level set위의 points들을 효율적으로 식별하는 것을 목표로 합니다.
이를 위해 training 카메라 pose에서의 Gaussian Depth Map에 의존성을 가지도록 설계하였습니다. 해당 Depth map은 Gaussian Splatting Rasterizer를 extending하여 얻어 질 수 있으며, 본 논문에서는 해당 Depth map으로부터 level set의 point들을 적절하게 sampling하는 방법을 소개합니다.
이 기법은 Marching Cube기법에 비해 scalable하고 single GPU에서 수분내로 surface mesh를 생성하게 되는데 Neural SDF로 mesh를 추출하는데 24시간이 걸리는 것에 비해 엄청나게 빠른 속도입니다.
[문제점3] mesh화하면서 랜더링 퀄리티가 떨어집니다.
[해결방안3] Gaussian Splatting rendering만을 사용해서 mesh와 3D Gaussian들을 optimize하는 optional한 refinement 기법을 소개합니다. 이를 통해 mesh에 기반한 radiance field모델 보다 높은 퀄리티로 Scene을 랜더링합니다.
Contribution
논문에서 언급하고 있는 Contribution은 3가지 입니다.
- 정확한 Geometry를 획득 할 수 있게 3D Gaussian과 Surface를 Align해주는 Regularization Term
- Gaussian에서 정확한 Mesh를 몇분 내로 추출하는 효율적인 Algorithm
- Gaussian Splatting Rendering으로 Surface에 위치한 3D Gaussian와 Mesh를 optimization하는 Gaussian-Mesh Binding 기법
3D Gaussian과 Surface의 Alignment
Gaussian이 flat하게 Surface에 배치 될 수 있다라는 가정을 두고 설계되었습니다. 우선 가우시안들로 surface를 표현하기 위해, 가우시안의 alpha값은 1로 셋팅됩니다. 그리고 아래 Regularization Term을 통해 Gaussian을 Flat하게 만듭니다.

(Peer-Review없이 수식을 개인적으로 해석한 것이라 잘못된 부분에 대해 과감한 코멘트 부탁드립니다.)

일반적인 가우시안은 A와 같이 Elipse 중간의 밀도가 높고 중앙에서 멀어질수록 밀도가 낮아지는 형태입니다. 수식은 아래와 같습니다.

본 논문에서 제시하고 있는 가우시안의 수식은 B와 같이 가장 짧은 반지름(S)의 방향을 기준으로, 멀어지면 밀도(d함수:density)가 낮아지는 형태입니다. 타원에서 멀리있는 점이더라도, 짧은 반지름 방향에 대해서는 떨어진 거리가 짧다면 밀도가 높게 됩니다.
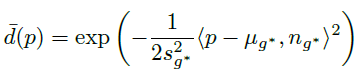
B형태로 설계할 경우, Surface를 표현하기 위해 타원이 납작해지게 됩니다. 하지만 렌더링은 A형태가 되어야 자연스럽게 Scene을 표현 할 수 있습니다. 때문에 Sampling한 point p 에 대해 A가 B의 특성을 갖도록 ' surface를 기준으로 떨어진 distance인 함수f'의 차이로 Loss가 설계되었습니다.
f를 구체적으로 보자면,
- A에 대한 f함수는 카메라 포즈에 대해 Gaussian Rasterizer로 Depth Map을 획득하고, 샘플링한 point p와 depth map의 차이로 계산됩니다. depth map은 일정 density이상일 경우에 surface로 인지하고 만들어질 것이라 생각됩니다. 이렇게 설계하면 surface가 0이고 surface 밖으로 멀어지면 +, Surface 안쪽으로 깊어지면 -형태인 SDF(Sign Distance Function)이 됩니다.
- B에 대한 f함수는 아래 수식으로 SDF(Sign Distance Function)로 정의됩니다.
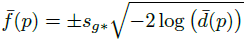
graph로 그려보면, sampling한 point p에 대해 밀도(d)가 작아질 경우(=표면에서 멀어질 경우) 값이 커지는 형태입니다. 반대로 density가 1이면, 표면이기 때문에 SDF값이 0이 됩니다.

여기까지가 Regularization Term에 대한 설명이고, 별도로 SDF의 Normal값(수직인 벡터)로 만들어지는 Normal Regularization Term이 더 있습니다. (Norm이 보통 Normalization의 약자로 쓰이는데 여기에선 Normal의 약자로 보입니다.)
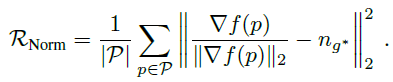
시그마 안의 왼쪽은 A에 대한 f함수에 관한 식으로, Scalar인 SDF함수의 gradient를 계산하고 L2-Norm으로 나누어 Vector형태로 만들어집니다. 시그마 안의 오른쪽 n은 같은 형태로 B의 f함수에 관한 normal값입니다. 샘플링한 point에 대해 A와 B의 Normal값이 갖도록 만들어주는 Loss로 보여집니다.
Mesh Extraction
1. surface에 해당하는 density level parameter λ을 0.3으로 정의합니다. surface라고 간주되는 density의 범위입니다.
2. density level에 해당하는 points들을 sampling합니다.
3. Poisson Reconstruction을 수행합니다. Poisson Reconstruction은 Point Cloud를 바탕으로 Detail한 3D Mesh를 구성하는 알고리즘이며, 이전글참고 바랍니다. 여기서 Octree의 depth는 10으로 설정했습니다.
Poisson Reconstruction을 위해 density level λ에 해당하는 Point들을 효율적으로 샘플링해야 합니다. training 카메라 포즈로 그려지는 Gaussian의 depth map을 다시 사용합니다.
1. depth map을 바탕으로 pixel을 랜덤하게 샘플링하고 ray를 그립니다.
2. n개의 p+tv좌표의 point들을 샘플링합니다. p는 depth map의 point이고, t는 가우시안의 표준편차 -3σ, +3σ , v는 line의 direction입니다. p를 기준으로 line을 따라 일정 interval을 갖고 n개의 포인트를 샘플링한다는 의미로 보입니다. 아래 초록색 부분에 해당합니다. depth map을 통한 surface는 정확하지 않기 때문에, 표준편차 구간을 두고 샘플링하는 것으로 생각됩니다.

3. 아래 density 계산식을 통해 point "p+tv"의 density를 계산하고 density level λ에 속하는지를 판단하게 됩니다.

4. (이부분은 이해가 안되는데) n개의 density에 대해 아래를 만족하는 경우,
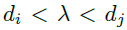
λ를 가지면서 카메라에 가장 가까운 점 p+tv를 linear interpolation을 통해 찾을 수 있습니다. 이 점에 대해서 따로 언급이 없는데 카메라의 가장 가까운 point들도 샘플링한다는 의미로 보입니다.
위와 같이 샘플링을 하고 나면 Poisson Reconstruction 단계에서, 샘플링한 point에 대한 Normal값이 필요한데, density를 사용해서 아래 수식으로 normal값을 계산합니다.

New 3D Gaussian을 Mesh로 Buinding
[해결방안3]에서 언급됬던 Refinement 단계에 해당하며 mesh에 color를 입히는 단계로도 볼 수 있습니다. Gaussian Splatting Rasterizer를 사용해서 Gaussian과 Mesh를 연결하고 이 둘을 같이 optimization하게 됩니다. 이전 단계에서 Mesh가 만들어지면, Mesh 위로 3D Gaussian들이 인스턴스화됩니다. (참고로 인스턴스화라는 용어는 프로그래밍에서 class를 메모리로 올려서 실체화 할 때 사용됩니다.) 이 과정 후 Gaussian은 더 이상 3D형태가 아니라 triangle위의 2D형태가 됩니다. n개의 얇은 3D Gaussian들을 아래와 같이 Mesh를 구성하는 각 triangle의 surface로 매칭시킵니다. 정확히 언급되지 않았지만 어떤 triangle를 포함하는 Gaussian들이 해당 triangle로 맵핑 되는 것으로 생각되어집니다.
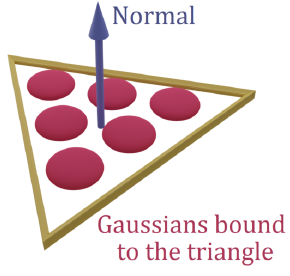
이 매칭을 위해서, 기존 3D Gaussian Splatting(3D-GS)에서 Gaussian의 learnable parameter인 mean, rotation, scale, opacity, SH의 설계가 바뀝니다.
- Optimize시, triangle의 vertex를 기준으로 무게 중심좌표계로 가우시안의 중점(=mean) 위치를 표현합니다.
- 이전 단계까지는 3D-GS 방식을 그대로 따르고 있고 scaling에 해당하는 변수는 총 3개(x,y,z)이고, rotation에 해당하는 변수는 quaternion으로 설계 되어 있습니다. 하지만 Refinement 단계에서는 가우시안들을 평평하게 만들기 때문에, scaling에 해당하는 변수가 2개이고 rotation에 해당하는 변수도 2D rotation 변수를 복소수(complex number) 하나로 표현하게 됩니다. 아래는 복소수의 예시입니다 (그림 출처 : link).
- opacity value와 SH(Sperical Harmonics)는 기존 3D-GS와 동일하게 설계됩니다.

여기까지 읽고나면 궁금증이 생깁니다. Gaussian의 Scale factor가 3개에서 2개로 바뀔수는 있을 것 같은데, Gaussian의 형태가 3D 타원에서 2D타원으로 변경된다고 해도 3D공간상에 위치한 2D 타원이기 때문에 Rotation Matrix가 3D Rotation이 되어야 되지 않는가 생각됩니다.
힌트를 Appendix에서 얻을 수 있습니다. refinement단계에서, 본 논문에서 제시하고 있는 복소수 형태의 2D rotation을 matrix형태의 3D rotation으로 바꾸는 방법에 대해 소개하고 있습니다. 이 과정이 필요한 이유는 학습과정에서 3D rotation matrix를 사용해서 Gaussian Rasterizer를 계산해야하기 때문이라고 합니다.

triangle의 normal과 edge가 3D Rotation정보를 갖고 있고, triangle을 바탕으로 2D 타원이 3D 공간상에 배치 되는 것을 볼 수 있습니다.
Experiments
구체적인 학습 방법입니다. 아래에 언급되는 시간은 Tesla V100에서 측정되었습니다.
3D Gaussian 생성
1. Regularization Term없이 7,000 iteration을 3D-GS방식과 동일하게 학습합니다.
2. Opacity에 추가적인 Entropy Loss를 추가해서 0 또는 1값에 가까워지도록 2000 iteration을 학습합니다.
3. opacity가 0.5이하인 Gaussian들을 모두 제거합니다.
4. Regualization Term을 적용해 6,000 iteration을 수행합니다.
1~4단계를 모두 합치면 총 15,000 iteration으로 학습됩니다. 특정 point의 density 계산시, point에서 가까운 16개의 gaussian의 density값을 사용하였고 500 iteration마다 가까운 gaussian의 list를 업데이트하였습니다.
이 과정은 15~45분 정도 소요됬습니다.
Mesh Extraction
Scene에 bounding box를 그려서, bounding box안쪽과 바깥쪽을 나누어 각각 Poisson Reconstruction을 수행했습니다. Scene마다 bouding box를 그릴 수 없는 경우도 있을 수 있는데, bounding box를 그릴 경우 퀄리티가 더 좋았다고 합니다.
Mesh의 resolution을 줄이기 위해 quadric error metrics를 사용한 mesh를 simplification적용 했습니다. SIGGRAPH 1997 연구라고 합니다.
이 과정은 5~10분 정도 소요됬습니다.
Joint Refinement
2,000, 7,000, 15,000 iteration 중에 1번 mesh와 gaussian을 refine했습니다. iteration에 따라 몇분에서 1시간까지 소요됩니다. 2,000과 7,000 iteration을 사용한 이유는 Ablation Study에 있습니다.
다음으로 실험 결과입니다.
Mip-NeRF360데이터셋(이전글)을 사용했습니다. PSNR / SSIM / LPIP에 대해선 이전글 참고바랍니다.
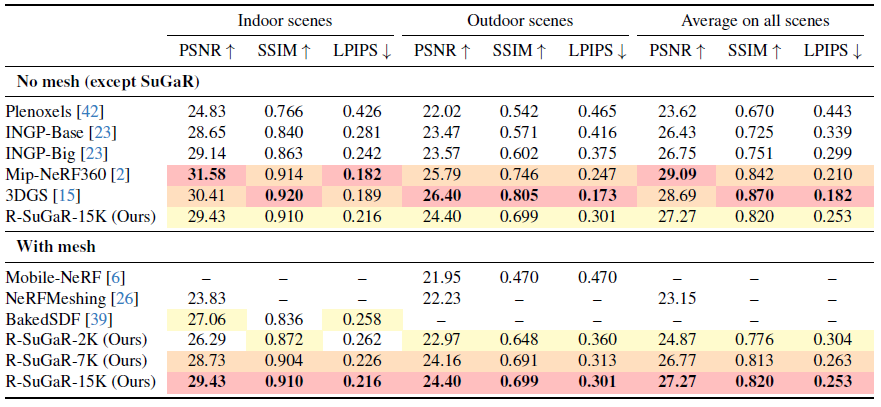
Mesh 적용 전 단계에선, base연구인 3DGS보다 낮은 성능을 가집니다.
Mesh 적용 후 단계에선, mesh화한 연구들 중에는 가장 높은 성능을 보이는 것을 볼 수 있습니다. 여기서 특이한 포인트는 mesh화 전/후 단계에서 성능이 동일하다는 점입니다. Mesh를 높은 퀄리티로 reconstruction하고, Surface 가까이에 Gaussian들이 잘 배치된 것이라 생각 해 볼 수 있습니다.

marching cube 알고리즘(이전글)을 적용했을 경우, Poisson Reconstruction시 sampling되는 point들을 Gaussian의 중점들로 사용했을 경우, Surface Density level을 0.1~0.5로 변경 하였을 경우를 나타냈습니다. 0.5로 할 때 가장 좋은 성능을 보이는데 왜 0.3을 기본으로 했는지 모르겠네요.
Ablation Study

triangle의 갯수에 따른 퀄리티 실험입니다. 본 연구에서 제시한 3DGS로 mesh의 triangle을 구성하게 될 경우, vertex 갯수를 늘이면 퀄리티가 높아집니다.
전통적인 triangle rasterization을 사용한 UV Texture방식을 적용할 경우 성능이 낮아지며, 이 경우에는 vertex의 갯수가 적어질 경우 오히려 성능이 높아집니다.

1번째 줄은 200K, 두번째 줄은 1M결과 입니다. Vertex수가 많아지면 퀄리티가 높아지는 반면, texture가 없는 Mesh는 Vertex수가 적은게 퀄리티가 높아짐을 볼 수 있습니다. low-polygon mesh가 surface를 regularization하는 효과를 갖기 때문입니다.

논문 pdf파일을 확대해서 캡쳐했습니다. 클릭해서 보시길 바랍니다.
2,000 iteration에서도 높은 퀄리티를 보입니다. 2,000 iteration이면 Regularization Term도 적용되기 전 단계입니다. Surface gaussian이 model을 optimizing하는데 excellent initialization을 가진다고 표현하고 있습니다. refinement단계가 missing되는 디테일들을 잘 잡아내는 역할을 하고 있다고 볼 수 있습니다. 당연히 추가적인 iteration을 통해 더 디테일한 퀄리티를 잡아내게 됩니다.
Closing..
내용 어렵네요.. 반복해서 읽었는데, 읽을 때마다 이해한만큼 다르게 해석되서 어려웠습니다. 이번 리뷰는 제가 잘못된 정보를 전달할까봐 걱정이되는 부분이 있습니다. 완전히 다른 의미로 전달된 내용이 있을 수 있으니 의심하면서 보시길 바랍니다.
그래픽스 개념이 많이 들어가네요. Text-to-3D연구들을 보면서 Stable Diffusion 모델들을 알아봐야겠다고 생각하는 것도 몇일 전인데, 이번 논문을 읽으니 그래픽스 기초와 수학 공부해야겠다는 생각이 들면서, 공부할게 끝이 없다고 생각됩니다.
이 기법을 사용하면 3D-GS보다 Floater들이 많이 잡히지 않을까 싶습니다. 이 연구를 토대로 재밌는 시나리오가 많이 만들어지길 기대합니다.
'3D-GS' 카테고리의 다른 글
| [논문 리뷰] DISTWAR (arXiv2023) : 3D-GS 학습 속도 개선 (3) | 2024.01.27 |
|---|---|
| [논문 리뷰] A Survey on 3D Gaussian Splatting (Jan 2024) (4) | 2024.01.17 |
| [코드 빌드] Dream Gaussian : Image to 3D, Text to 3D (12) | 2023.11.15 |
| [논문 리뷰] Dream Gaussian (ICLR 2024) : Image to 3D, Text to 3D (7) | 2023.11.08 |
| [논문 리뷰] 4D Gaussian Splatting (CVPR 2024) : Dynamic Scene 랜더링 (3) | 2023.10.23 |




댓글