[개념 정리] Diffusion Model 과 DDPM 수식 유도 과정

이전글 에서 Diffusion Model과 DDPM(Denosing Diffusion Probabilistic Model)의 개념에 대해서 알아봤습니다. 이번 글에서는 수식 유도 과정을 다뤄보겠습니다.

이전글에서 Diffusion모델은 Noise를 주입을 위해 사용되는 확률분포q와 Noise를 제거하는 확률분포pθ로 설계되어 있고, 확률분포 q에서 관측한 값으로 확률 분포pθ의 likelihood를 구하였을 때, 그 likelihood값이 최대(Maximum)가 되는 확률분포를 찾는 Maximum Likelihood Estimation 문제라고 언급했었습니다. -log를 붙여 최대화가 아닌 최소화하는 식으로 Loss가 설계됩니다.

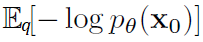
위 수식이 어떻게 아래 Diffusion Model 수식의 Loss로 도출 되는지 확인 해보겠습니다.

 

 

 

 

 

Evidence Lower Bound (ELBO)를 계산하는 문제로 변환

아래는 VAE(Variation Auto Encoder) 기본 개념서 내용(link)입니다. x0 대신 x 가 사용되고 xT 대신 z가 사용되었습니다. log앞에 마이너스가 빠졌습니다. 아래 수식에 한해서만 다시 최대화 문제입니다.

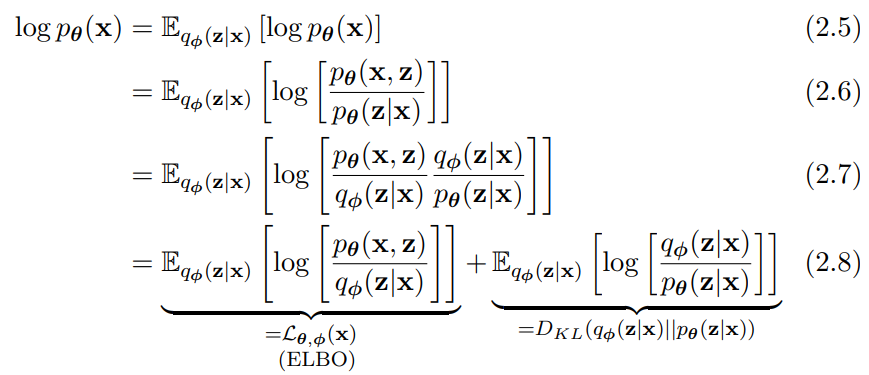
(2.5) 확률분포 q(z|x)로 샘플링하였을 때의 기댓값을 의미하는 기호가 앞에 붙었습니다.

(2.6) 아래 베이즈 룰에 의해서 변환됩니다.

(2.7 - 2.8) 분모 분자에 q(z|x)를 곱해주고 log성질에 의해 두개로 분할됩니다. 최종식의 오른쪽식은 q(z|x)를 반복 수행했을 때 기대값(Expectation) 이므로, E기호는 Summation식으로 바뀌고 최종적으로 KL Divergence식으로 바뀔 수 있습니다.

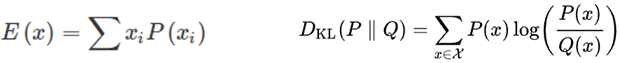
q(z|x)는 계산이 가능하지만, p(z|x)는 계산이 불가능합니다. KL Divergence 값은 항상 0 이상의 양수를 만족하는 성질을 이용하여,  (2.8)의 왼쪽식이 Evidence Lower Bound (ELBO)가 되어 ELBO를 최대화는 문제를 풀 수 있습니다. 아래에 다른 기호로 정리된 수식을 보면, (2.8)의 우측식이 사라지고, 좌측식과 유사한 형태가 남은 것을 볼 수 있습니다.

기호가 바뀌면서, log안의 분모 분자가 많이 바뀌었는데요. log안의 분자는 x0와 xT가 동시에 나올 확률이고, log안의 분모는 x0가 주어질 경우, xT가 나올 확률이기 때문에, Markov성질을 가지는 아래 수식으로 인해 위와 같이 변형 된 것을 짐작 할 수 있습니다. 

pθ는 reverse procss를 하기 때문에 prior가 t, posterior가 t-1이고 q는 forward process이기 때문에 반대입니다.

 

 

 

 

Diffusion Model Loss 도출

위 수식을 풀어보겠습니다.

(1) 마이너스가 빠지고 분자,분모가 바뀌었습니다.

(2) 직전에 언급된 Markov 성질에 의한 수식에 의해서 변환 됩니다.

(3-4) log성질에 의해 변환됩니다.

(5) 계산 가능하게 수식을 풀어주기 위해, 시그마(Σ)가 있는 수식 분자인 q의 prior에 x0를 추가해줍니다. 해당 q에 관한식은 prior가 x0로 부터 오기 때문에 같은 수식입니다. 최초 Diffusion Model(2015)에 Appendix B.3에는 단순히 Markov process에 의해서라고만 표기되어 있습니다.

(6) 아래 베이즈 정리에 의해 변환됩니다.

(7-9) 단순히 log성질에 의해 변환됩니다.

(10) KL Divergence 공식으로 정리됩니다.

이번글에서 수식 유도 과정만 정리합니다. 의미는 이전글 참조 바랍니다.

 

 

 

 

 

DDPM(Denosing Diffusion Probabilistic Model) Loss 도출

DDPM에서는 최초 Diffusion Model에 기반하여 Neural Network로 학습시키기 위해 수식을 간략화 했습니다.

조금 전에 본 위 수식이 아래 수식으로 어떻게 바꾸었는지 살펴보겠습니다.

LT 파트는 Regularization Loss에 해당하며, R Noise 주입정도를 나타내는 Parameter인 β가 fixed되어 학습이 되지 않기 때문에 제거됩니다. L0 파트는 전체적으로 봤을 때 영향력이 적기 때문에 제거 됩니다.

최종적으로 Lt-1 파트를 최소화 하도록 계산하면 됩니다. KL Divergence의 수식을 살펴보면 아래와 같이 됩니다. 

마지막 수식에서 표준편차(σ)는 학습 parameter가 없어서 상수가 되므로 버리고, q(xt-1|xt,x0)의 평균(μ)과 pθ(xt-1|xt)의 평균(μ)에 대해 위 식이 최소화가 되도록 pθ 네트워크를 학습시키면 됩니다. 때문에 Loss는 아래와 같이 정리 됩니다.

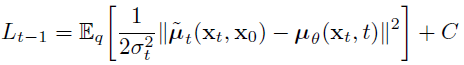
아래에서 q(xt-1|xt,x0)와 pθ(xt-1|xt)의 평균을 계산하여 Loss를 산출해보겠습니다. 그 전에 수식 증명에 필요한 q( xt | x0 ) 을 먼저 보겠습니다.

 

 

 

 

 

q( xt | x0 )  계산

최초 상태(x0)가 주어졌을 경우, 특정 시점의 상태(xt)가 나올 확률분포에 대한 식입니다.

q는 아래 수식으로 정의되고,

아래 기호로 재 정의하며,

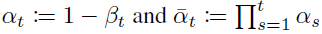
 X가 Normal(=Gaussian) Distribution을 따를 때, 평균(μ) + 표준편차(σ) * Normalized 가우시안 분포(ϵ)의 식으로 나타낼 수 있는 아래 Reparameterization Trick을 사용하면,

xt는 아래와 같이 정의 될 수 있습니다.

위 수식은 아래와 같이 계산됩니다.

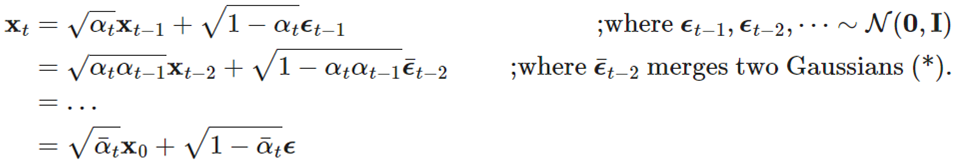
결과적으로, 아래와 같은 수식이 만들어집니다.

 

 

 

 

 

 

q( xt-1 | xt, x0 ) 평균 계산

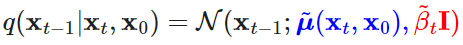
로 정의하고, 평균을 구해보겠습니다.

첫 번째 줄은 베이즈 정리에 의해 변환됩니다.

두 번째 줄은 아래 3가지 수식을 사용해서 계산됩니다.

1) 아래 수식은 이전글 에서 Diffusion Model의 q가 아래와 같은 확률분포를 따른다고 했었습니다.

2) 앞에서 β를 α와 α헷 으로 재정의 했었습니다.

3) q는 Gaussian Distribution을 따릅니다. 확률 밀도 함수(pdf: probability density function) 수식은 아래와 같습니다.

자세한 수식 설명은 생략하겠습니다.

세 번째, 네 번째 줄은 수식을 단순히 풀어 쓰고 정리되었습니다.

네 번째 줄을 해석하자면, C(xt,x0)는 x-1과 관련성이 없기 때문에 상수 처리되고, Gaussian Distribution의 pdf 위 수식에 의해 빨간색과 파란색 부분이 각각 표준편차(σ), 평균(μ)이 됩니다.

 

이를 정리하면 분산은 아래와 같이 정리되고,

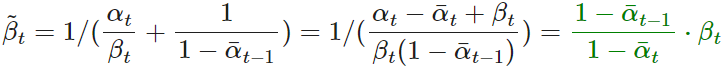
평균은 아래와 같이 정리됩니다.

위 수식을 종합하면, DDPM 논문에 표기된 아래 수식이 됩니다.

 

추가적으로 더 정리하자면, q( xt | x0 ) 계산 파트에서 정리된 아래 수식에 의해,

x0를 아래와 같이 변환 할 수 있습니다.

그러면 평균은 다음과 같이 정리됩니다.

최종적으로 다시 정리하겠습니다.

 

 

 

 

 

 

 

pθ( xt-1 | xt ) 평균 계산

로 정의하고 평균이 어떻게 정의되는지 보겠습니다. pθ는 q의 평균을 근사화하고자 합니다. q의 평균 식에서 xt는 입력값이고, α, α헷은 고정값입니다. 가우시안 분포(ϵ)를 따르는 네트워크를 시간 t에 따라 학습 시키기 위해서, 평균을 아래와 같이 정의해줍니다. 위 q( xt-1 | xt, x0 ) 의 식에서 변경된 부분은 ϵ입니다.

Normal Distribution 수식으로 다르게 정리하면 아래 수식과 같습니다. 분산의 표기 기호가 바뀌어져 있습니다.

 

 

 

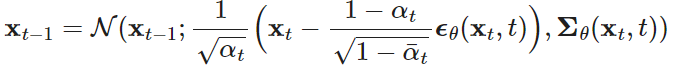
DDPM Loss 최종 계산

DDPM의 Loss는 아래 수식을 계산하면 된다고 했었습니다.

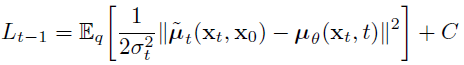
위는 확률분포 q로 샘플링하였을 때의 기댓값 식이고, 아래는 x0와 가우시안 분포(ϵ)로 샘플링하였을 때의 기댓값 식으로 표현되었을 뿐 같은 수식입니다. C는 상수로 없어졌습니다.

2번째 줄의 파란색과 초록색은 위에서 계산한 평균값들입니다. 이를 대입해주고 정리하면, 마지막 수식이 됩니다.

Loss를 계산하는 것이기 때문에 weight term을 제거해주어서 최종적으로 아래 수식이 Loss가 됩니다.

이상으로 본 글의 목표인 수식 유도 과정을 살펴 보았습니다.

 

 

 

마지막으로 DDPM 논문에 언급된 수도코드 의미를 언급하고 글을 마치겠습니다.

Training과정과 Sampling과정의 연관관계를 설명하자면,

먼저 Training과정에서 네트워크ϵθ 를 학습합니다. X0(=입력 이미지)는 forward process에 의해 XT(=노이즈 이미지)를 항상 일정하게 만들게 됩니다. Sampling과정에서는 XT가 학습된 네트워크ϵθ를 통해 X0(=새롭게 합성되는 이미지)로 만드는 방법에 관해서 다루고 있습니다.

 

<Training>

x0는 확률분포 q의 입력으로 주어집니다. t는 정수 T까지 정수값을 가집니다. ϵ는 가우시안 분포(=정규 분포)를 따릅니다. 아래 수식을 Neural Network의 weight를 update하기 위한 Loss로 사용합니다.

수렴 할 때까지 반복합니다.

 

<Sampling>

XT는 가우시안 분포(=정규 분포)를 따릅니다. t가 1보다 크면 z(=xt)는 가우시안 분포를 따르고, 아니면 0 이 됩니다. t-1번째 이미지는 t번째 이미지와 학습된 ϵθ에 의해 생성되어 집니다.

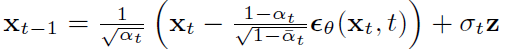
T step 반복합니다.

 

 

 

 

출처

글 : link 

유튜브 : link 

VAE 개념 책 : link